MATLAB矩阵操作详解：从基础到高级

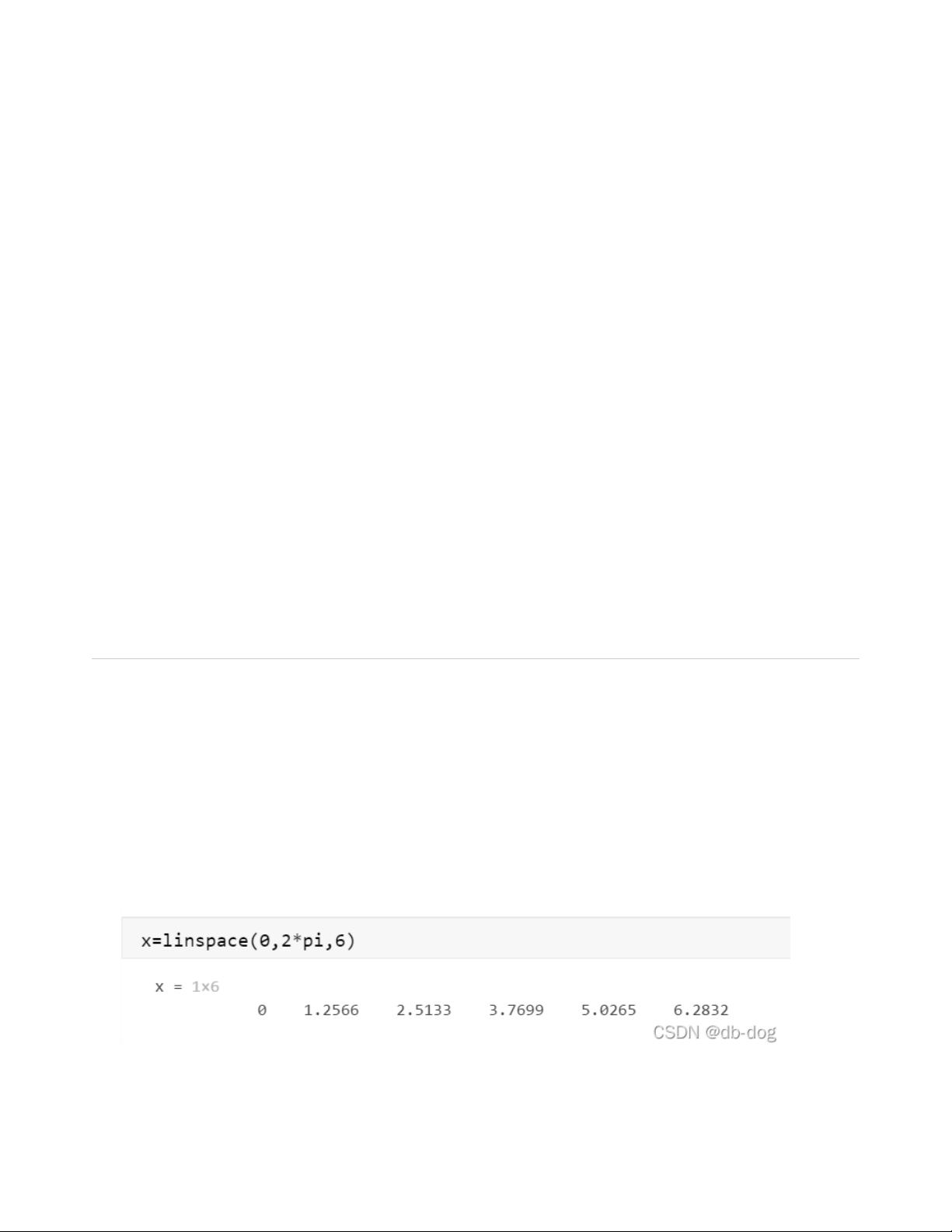
"这篇教程是MATLAB快速入门系列的第二部分，主要讲解矩阵的相关操作，包括冒号表达式、矩阵元素引用、矩阵运算、特殊矩阵和矩阵变换等内容。" 在MATLAB中，矩阵是基本的数据结构，对于理解和操作至关重要。本教程首先介绍了冒号表达式，用于创建序列。例如，`e1:e2:e3`可以生成一个等差序列，如果省略步长`e3`，默认步长为1。`linspace(a,b,n)`函数则用于生成从`a`到`b`的`n`个等间距点，如果不指定`n`，默认会生成100个点。 接着，教程讲解了矩阵元素的引用方式。在MATLAB中，矩阵按列存储，可以通过索引来访问特定元素。如`A(i,:)`表示第`i`行的所有元素，`A(:,j)`表示第`j`列的所有元素，`A(i:i+m,k:k+m)`则表示获取矩阵的一个子区域。`reshape(A,m,n)`函数可以改变矩阵的形状，使其成为`m`行`n`列的新矩阵，而元素总数不变。`A(:)`操作会将矩阵转换为一列向量。 在矩阵运算部分，教程涵盖了算术运算和逻辑运算。算术运算包括矩阵的转置、加法、减法、乘法、右除（/）和左除（\）、幂运算。例如，`A'`表示矩阵的转置，`A+B`表示矩阵的加法，`A./B`表示元素-wise的右除。逻辑运算涉及关系运算符（如`<`, `>`, `==`, `~=`）和逻辑运算符（如`&`, `|`, `~`, `xor`），它们可用于构建条件表达式或进行元素-wise的逻辑操作。 特殊矩阵部分介绍了一些预定义的矩阵函数，如`zeros(m,n)`生成`m`行`n`列的全零矩阵，`magic(n)`生成一个n阶魔方阵，其行、列和对角线上的元素和相等。还有`vander(v)`用于创建范德蒙矩阵，`hilb(n)`生成希尔伯特矩阵，`compan(p)`生成多项式的伴随矩阵，以及`pascal(n)`生成帕斯卡矩阵。 最后，教程提到了矩阵变换，其中对角阵是指仅对角线上有非零元素的矩阵，数量矩阵是对角线上元素相同的矩阵。这些概念和函数在处理特定类型的线性问题时非常有用。 总结来说，这个MATLAB快速入门教程的第二部分主要聚焦于矩阵的创建、操作和应用，是学习和理解MATLAB基础的重要资源。通过掌握这些知识，用户将能够更有效地在MATLAB环境中进行数据处理和计算。