解对策问题：从《取石子》看两种思路

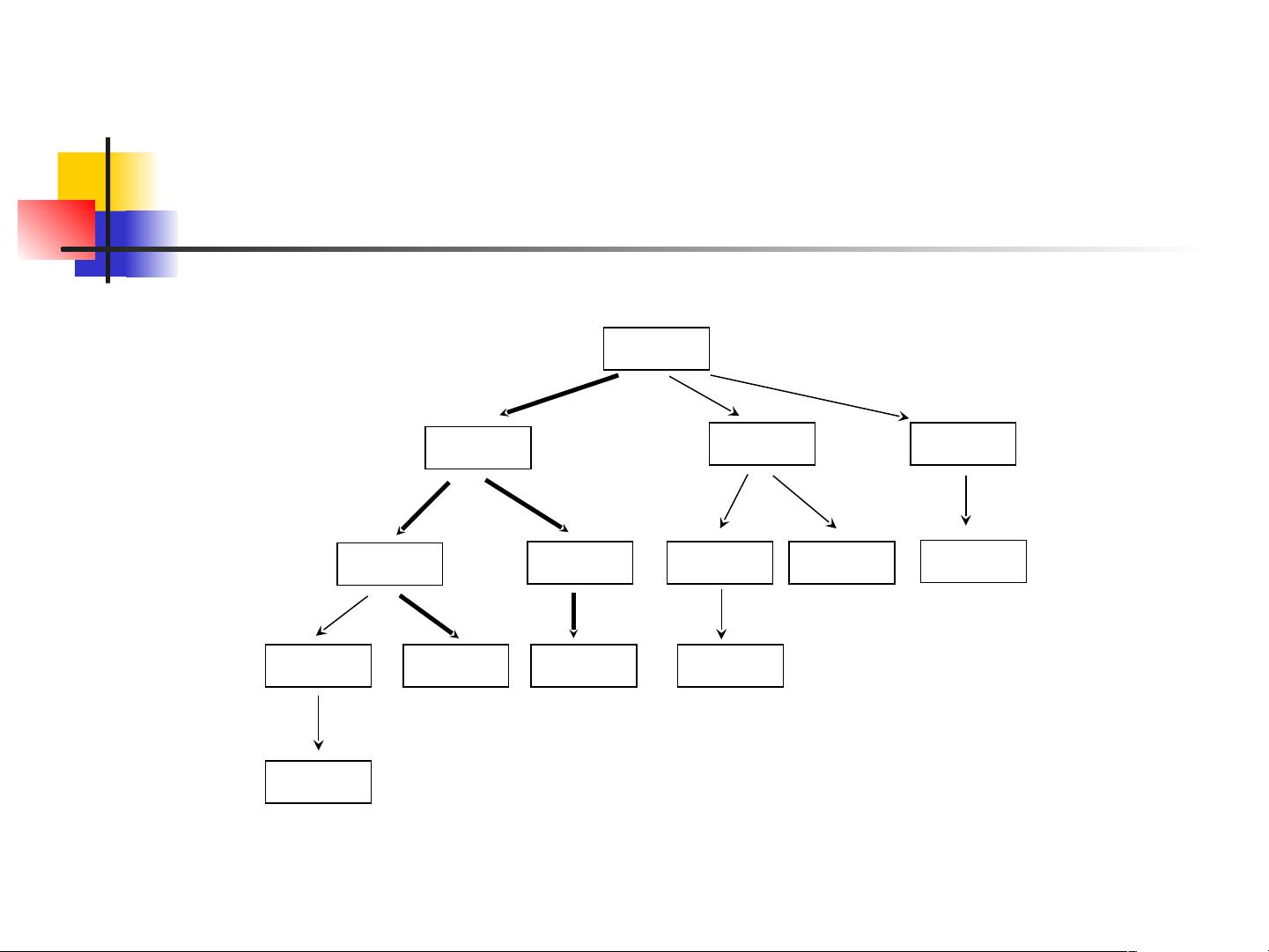
"这篇文章主要介绍了对策问题的解决思路，通过《取石子》问题作为案例进行深入解析，涉及运筹学中的对策论和动态规划等概念。" 文章中提到的对策问题，通常出现在ACM/ICPC这类编程竞赛中，涉及到两个玩家在考虑对方最优策略的情况下，寻找自身的必胜或必败策略。这类问题的关键在于理解和应用动态规划及图论的思想。 首先，对策论是运筹学的一个分支，主要研究在不确定性和竞争环境下，参与者如何做出最佳决策。在《取石子》问题中，甲乙两人轮流取石子，目标是避免成为最后一个无石子可取的人。这种问题的解决方案通常基于两个核心因素：当前石子总数N和当前最多可取的石子数K。 解决对策问题的两种基本思路在文章中通过状态转移的拓扑结构得以展现： 1. **自顶向下构造**：从初始状态（N，N-1）开始，递归地分析所有可能的子状态。如果甲在某一步操作后，无论乙如何操作，甲都能确保获胜，那么甲在当前状态就有必胜策略。反之，如果乙总能找到让甲输的方法，那么甲在当前状态就必败。 2. **动态规划**：这是一种自底向上的方法，通过构建一个状态表来记录每个（N，K）状态的胜负情况。从最小的状态开始，逐步填充表格，直到找到初始状态的胜负情况。在这个过程中，对于每个状态，检查所有可能的子状态并确定最优解。 以N=4为例，初始状态（4，3）表示有4粒石子且最多可取3粒。通过分析所有可能的转移，我们可以看到无论甲取1粒、2粒或3粒，乙总能使得接下来的状态变为（1，1），这是一个先手必败的状态。因此，甲在初始状态（4，3）下没有必胜策略，即甲必败。 这两种方法在解决对策问题时各有优势。自顶向下构造直观易懂，但可能会有重复计算；动态规划避免了重复，提高了效率，但需要设计合适的状态和状态转移规则。 理解和掌握对策问题的解决思路对于参与ACM/ICPC等编程竞赛或者解决实际生活中类似博弈问题具有重要意义。通过深入学习和实践，可以提升逻辑思维能力和问题解决技巧。