数值积分与微分简介：MATLAB实现及应用

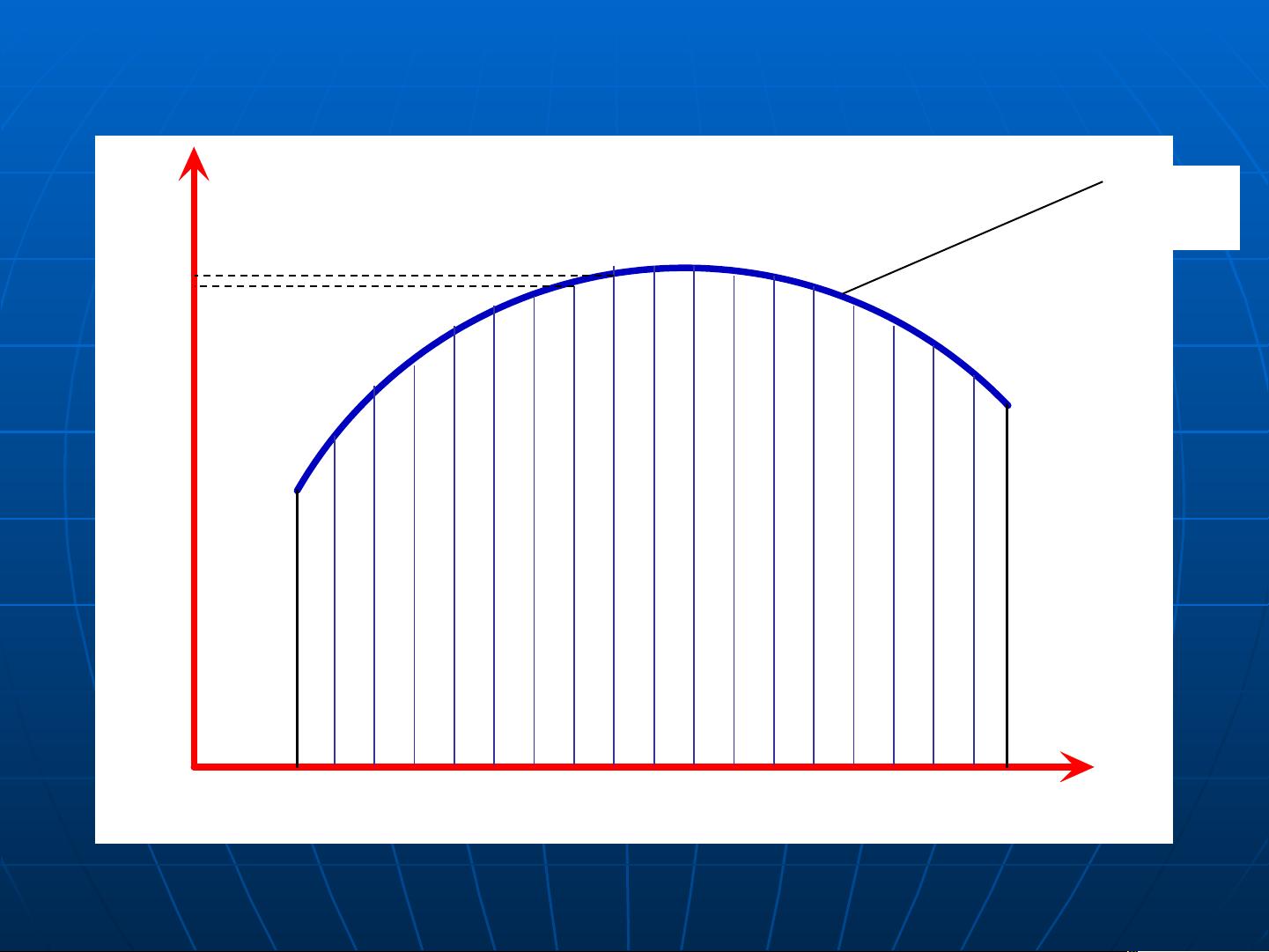
"该资源是关于数值积分与微分的PPT教程，主要讲解了如何在MATLAB环境下进行数值计算。由中南大学材料科学与工程学院的唐建国主讲，内容涵盖了数值积分的各种方法，如矩形积分、梯形积分、抛物线形积分、牛顿-科茨公式、自适应Simpson求积法以及高斯求积法。此外，还介绍了数值微分的相关知识，并提及了MATLAB中用于积分和微分的内置函数。" 在数学和工程领域，数值积分与微分是解决实际问题的重要工具。当遇到复杂的积分问题或者无法获得被积函数解析形式时，就需要采用数值方法来求解。在本讲座中，唐建国教授首先介绍了积分问题的重要性，比如在电磁学中的高斯定理和环路定理，这些都是基于积分原理的物理定律。 数值积分的核心是将连续的积分区间转化为离散点的函数值之和，以此来近似整个积分。这种方法不需要找到原函数，避免了寻找原函数的困难。讲座详细讨论了几种常见的数值积分方法： 1. **矩形积分近似**：将积分区间划分为多个小矩形，每个矩形的面积等于宽度乘以对应点的函数值，所有矩形面积之和即为积分的近似值。 2. **梯形积分近似**：在每个小区间内，函数可以用两端点的平均值作为近似，将区间分为若干个梯形，梯形面积之和即为积分近似。 3. **抛物线形积分近似**：通过三次样条插值，构建一条经过三个点的抛物线，用抛物线下的面积作为积分近似。 4. **牛顿-科茨公式**：包括了等距节点的插值多项式，如辛普森法则（Simpson's rule），它在三个点上构造二次多项式，通过这个多项式来积分。 5. **自适应Simpson求积法**：根据函数的变化情况动态调整区间划分，以提高精度。 6. **高斯求积法**：在特定节点上使用 Legendre 多项式，通过极小化误差函数来选择节点，这种方法通常能提供较高的精度。 数值微分同样适用于函数不可导或解析表达式未知的情况。它涉及到对函数的局部变化进行估计，如有限差分法，通过函数值在某一点附近的差异来近似导数值。 MATLAB作为一种强大的数值计算软件，提供了诸如`quad`、`quadgk`等函数用于数值积分，以及`diff`函数用于数值微分，使得这些计算变得简单高效。 本讲座深入浅出地讲解了数值积分与微分的基本概念和实用方法，并结合MATLAB的应用，为学习者提供了实践操作的指导。无论是理论研究还是实际应用，掌握这些数值计算技巧都是非常有价值的。