湖南大学2005-2009高等代数考研真题精选

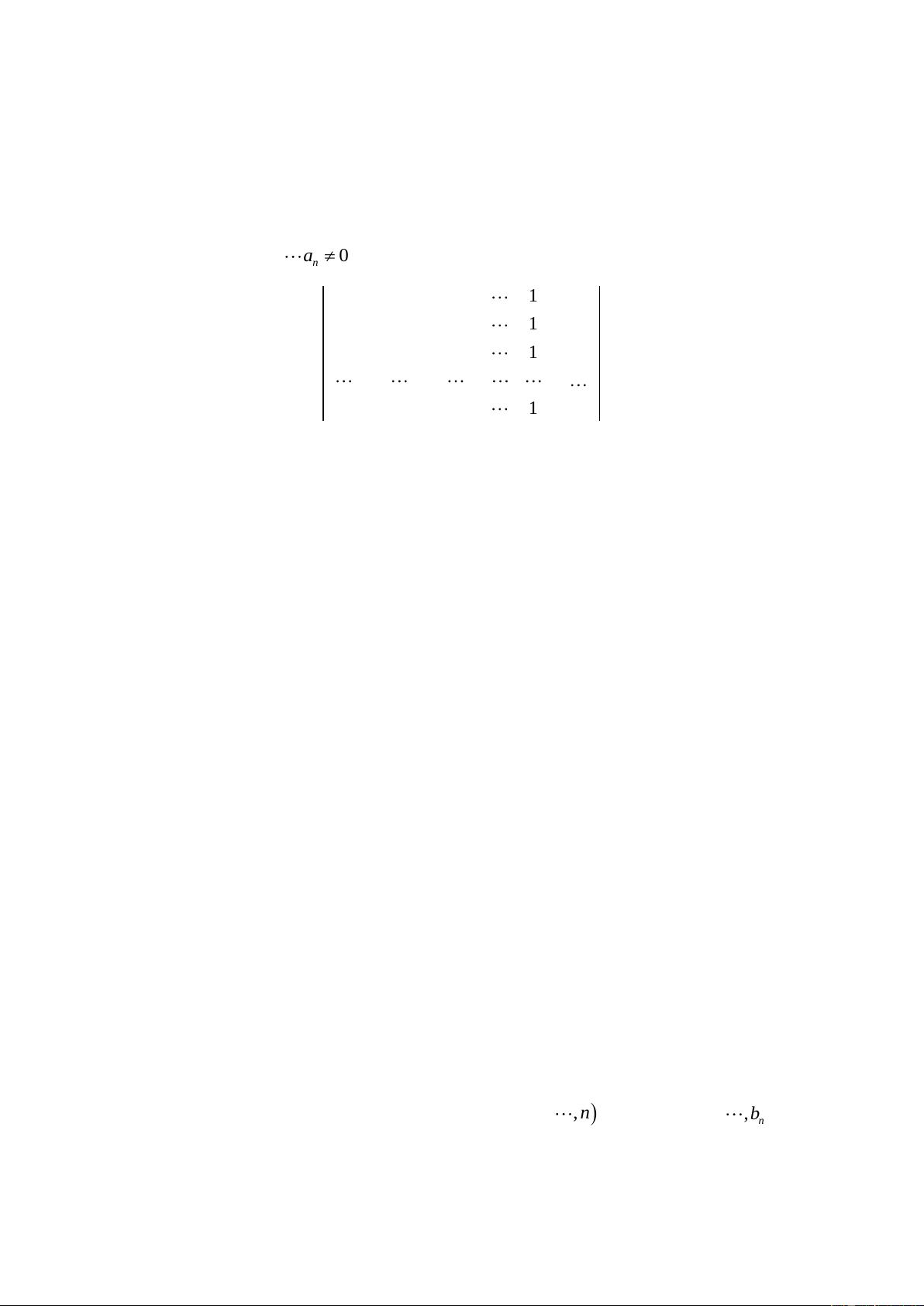
湖南大学高等代数2005-2009年考研真题涵盖了代数基础的多个重要概念和技能检验。这些题目涉及了多项式理论、行列式计算、矩阵运算、线性方程组解的存在性和唯一性、二次型、齐次线性方程组、复矩阵的特征值与标准形以及整系数线性方程组的性质。 1. **多项式整除定理**（第1题）: 提供了一个关于数域F上n次多项式f(x)与其导数关系的证明，必要条件是f(x)可以表示为一个常数倍的多项式减去它的导数，即f(x) = -n(ax+b)，其中a和b是F中的数。 2. **行列式计算**（第2题）: 要求计算一个特定的n阶行列式，这涉及到对特定矩阵的元素进行加法操作，这在矩阵理论中是基础技能。 3. **矩阵运算与分解**（第3题）: 求解矩阵A的幂次和与逆矩阵，以及矩阵乘积，这些都是矩阵代数中的核心内容。 4. **线性方程组解的性质**（第4题）: 通过分析线性方程组的系数，探讨了解的唯一性、无穷多解和无解条件，这涉及到了秩和系数矩阵的结构关系。 5. **二次型与向量空间**（第5题）: 实二次型的性质被用来推断是否存在特定向量使其二次型值为零，这是矩阵和向量空间理论的应用。 6. **齐次线性方程组与向量空间基础**（第6题）: 通过分析齐次线性方程组的解空间W，研究其与系数矩阵的关系，并求出标准正交基，这是线性代数中向量空间理论的重要组成部分。 7. **复矩阵特征值与标准形**（第7题）: 对复矩阵进行不变因子、初等因子和Jordan标准形的求解，这些是复数矩阵理论的基础，对于理解矩阵的对角化过程至关重要。 8. **整系数线性方程组的性质**（第8题）: 探讨整系数线性方程组的解与系数矩阵行列式的特殊关系，涉及到线性方程组解的整数性质。 9. **线性方程组与系数矩阵的性质**（第9题）: 对于一个特定线性方程组，若存在整数解，讨论系数矩阵行列式的特殊取值，这是线性代数中关于方程组整数解的特性。 这份湖南大学高等代数的考研真题集，不仅考察了考生的基础理论掌握，如多项式、行列式、矩阵运算、线性方程组等，还涵盖了代数中更深入的概念，如二次型、复数矩阵和整数解的特性和应用。这对于准备该考试的学生来说，是全面复习和提升代数能力的宝贵资源。