A.I. Maqueda et al. / Computer Vision and Image Understanding 000 (2015) 1–12 3
ARTICLE IN PRESS
JID: YCVIU [m5G;August 21, 2015;15:29]
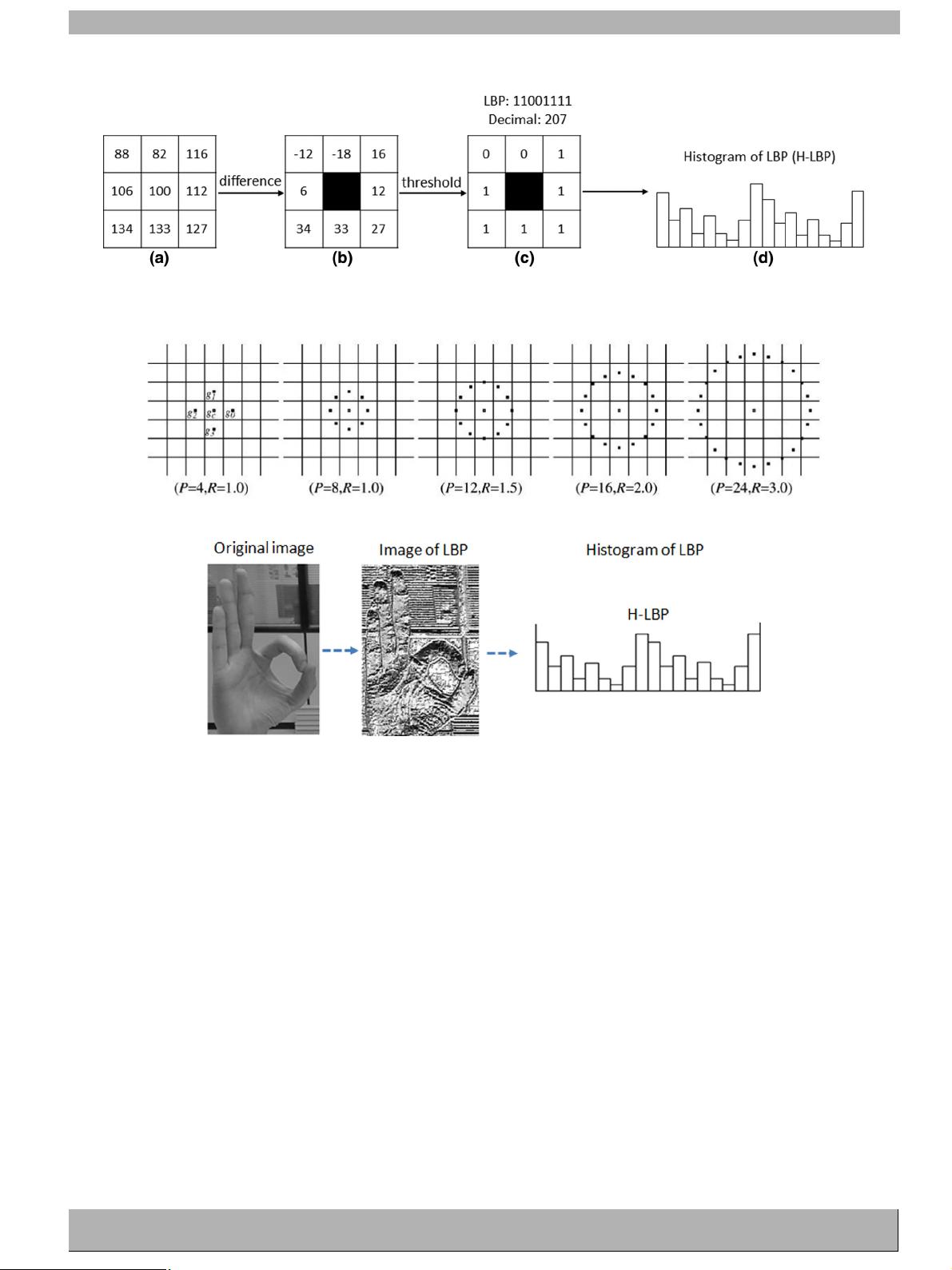
Fig. 1. Local binary pattern (LBP) from a pixel neighborhood. (a) 3 × 3 gray scale neighborhood. (b) Differences between the neighbor pixels and the center one. (c) Thresholded
neighborhood differences. (d) Histogram of LBP (H-LBP) from the whole image.
Fig. 2. Circularly symmetric neighbor sets for different P and R (extracted from [15]).
Fig. 3. Step 1: H-LBP computation.
2.2. S-LBP computation
The second step consists of extracting spatial information from
the image of LBPs, as shown Fig. 4. First, the coordinates of all the
LBP patterns that have contributed to a specific bin in the H-LBP his-
togram (representing a specific LBP type) are computed. From the al-
gorithmic viewpoint, this computation is not necessary as it is previ-
ously performed during the multi-scale LBP computation. Second, a
uniform sub-sampling of the image region coordinates is carried out,
obtaining a total of M × N sampled coordinates, defining M as the
number of rows, and N as the number of columns. The set of coordi-
nates of each LBP bin contributes to one histogram of M × N sampled
coordinates, which are called S
0
, S
1
,…, S
M×N−1
in Fig. 4, using a bilin-
ear interpolation. This way, a histogram of spatial coordinates is gen-
erated per each LBP bin of the computed H-LBP (spatial histograms).
As a result, we obtain 2
P
spatial histograms whose length is M × N,
where P was the number of neighbors in the LBP
P, R
. The H-LBP itself
and the set of spatial histograms are all concatenated to form a super-
descriptor called Spatiogram of Local Binary Patterns (S-LBP), whose
dimension is 2
P
+ [2
P
× (M × N)].
The S-LBP descriptor is highly discriminative since it contains both
local (the H-LBP) and global spatial information (histograms of spa-
tial coordinates of all the LBP patterns). The uniform sub-sampling of
the image coordinates allows to shorten the histograms length and
keep the computational cost manageable, establishing a trade-off be-
tween the computational cost and the discrimination ability. On the
other hand, the bilinear interpolation approach increases the robust-
ness against slight image translations, and the grid effect.
2.3. Temporal sampling
The last step consists of adding temporal information to the S-LBP
framework by carrying out a randomly and quasi-equally temporal
sampling scheme in the video sequence. Close images in time hardly
change their appearance, containing redundant information to iden-
tify the action that is being performed. This strategy also allows to
deal with variations in the execution speed of the hand gestures by
considering several sampling steps.
The randomly and quasi-equally spaced sampling is carried out as
follows. An additive random shift is applied to those images corre-
sponding to an equally spaced sampling in the temporal dimension
defined by
e
, as shown in Fig. 5.
The random shifting is performed following a discrete uniform
distribution over the considered maximum interval
max
.Onceall
the sampled images have been obtained, the S-LBP descriptors from
those selected images are concatenated to form Volumetric Spa-
tiograms of Local Binary Patterns.
Please cite this article as: A.I. Maqueda et al., Human–computer interaction based on visual hand-gesture recognition using volumetric spa-
tiograms of local binary patterns, Computer Vision and Image Understanding (2015), http://dx.doi.org/10.1016/j.cviu.2015.07.009









