图论基础：从七桥问题到现代应用

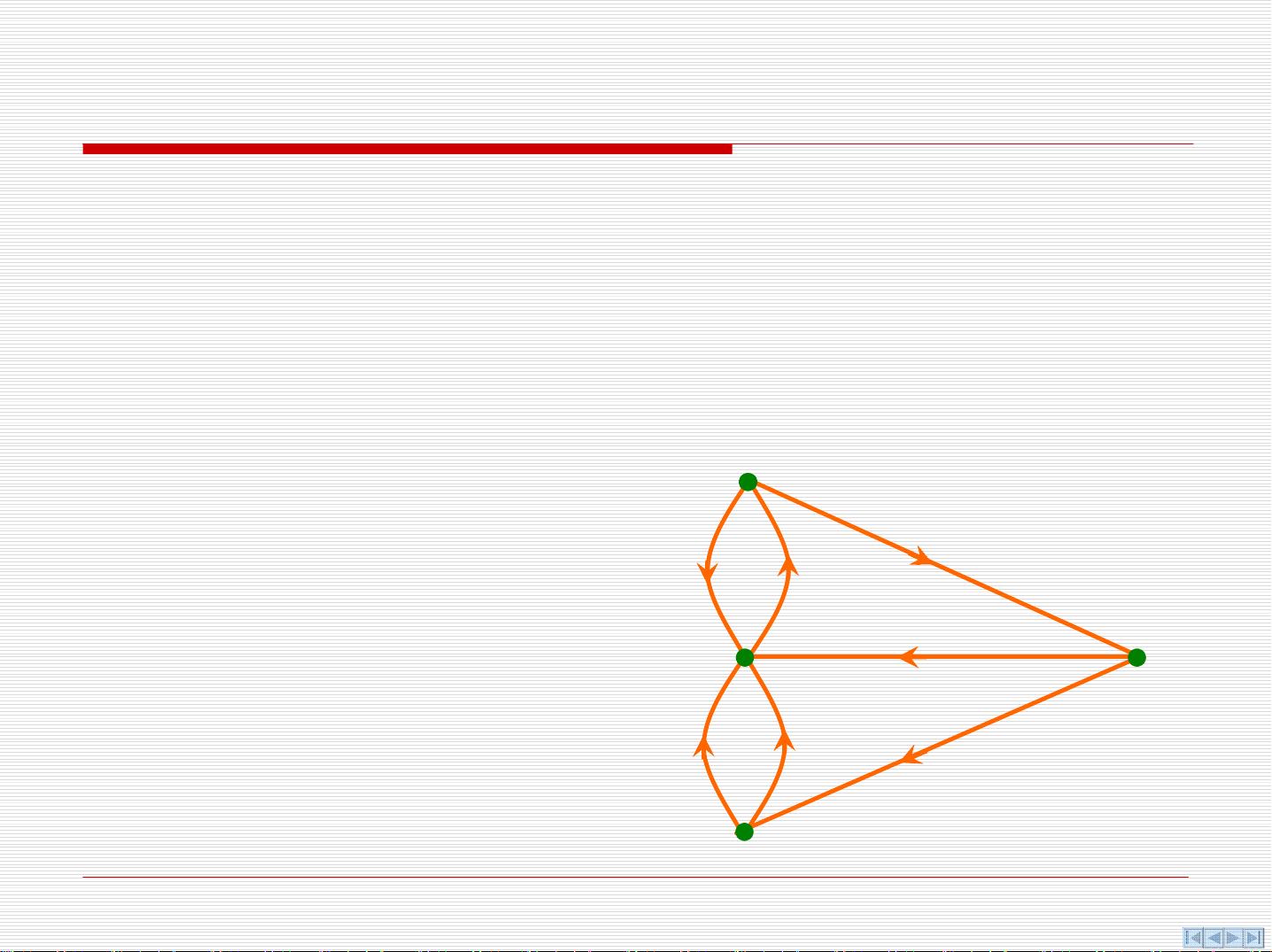
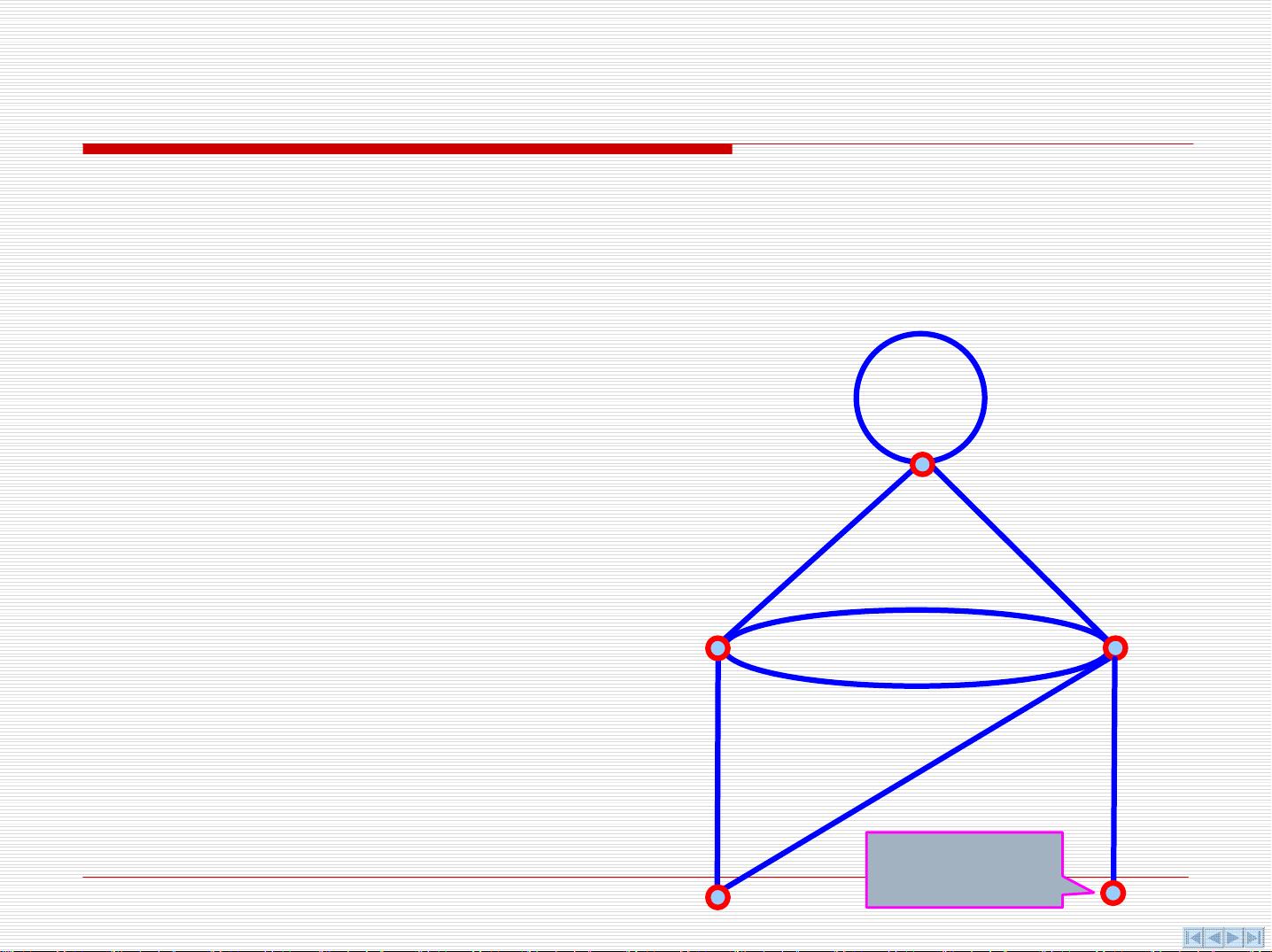
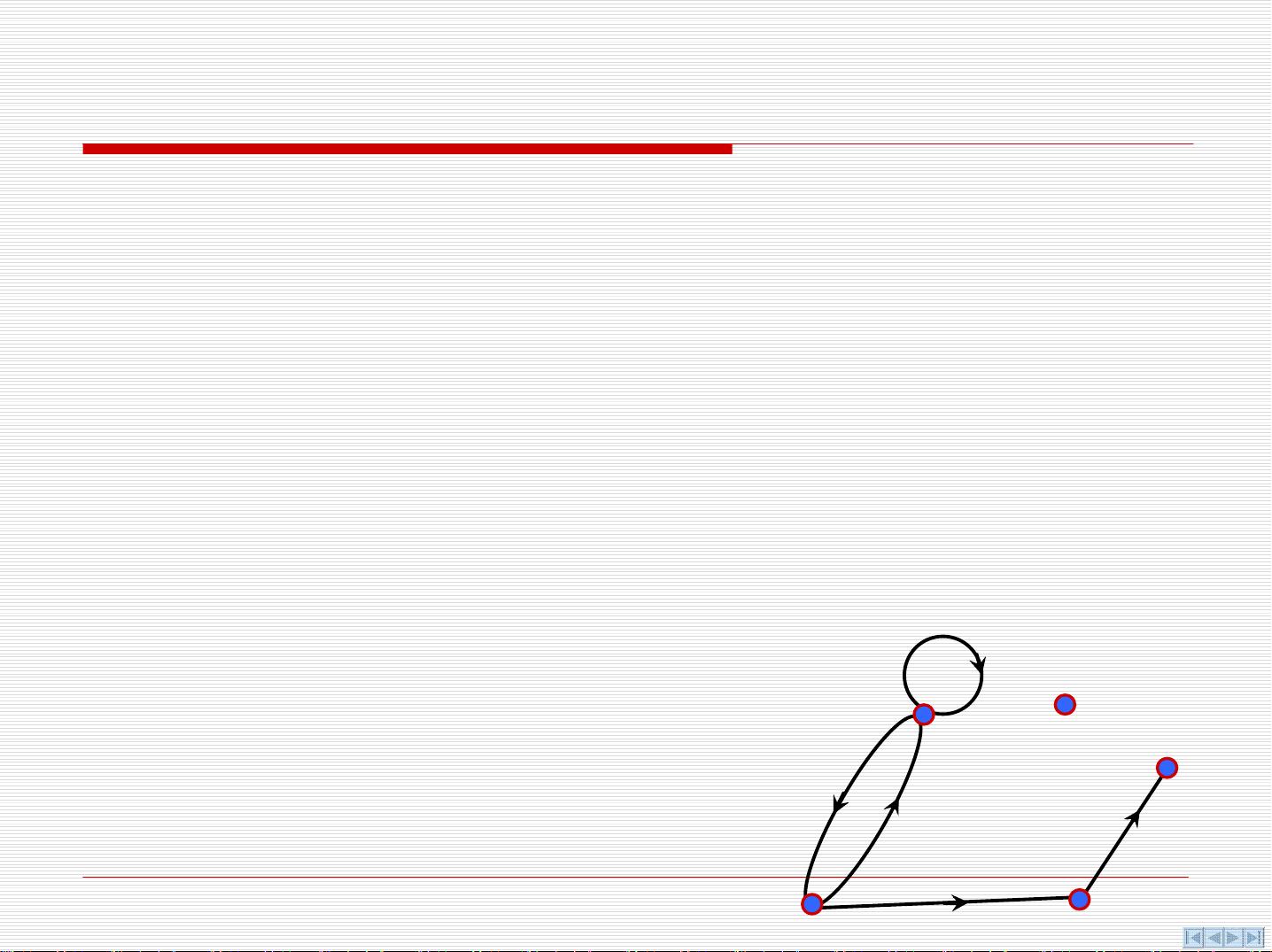
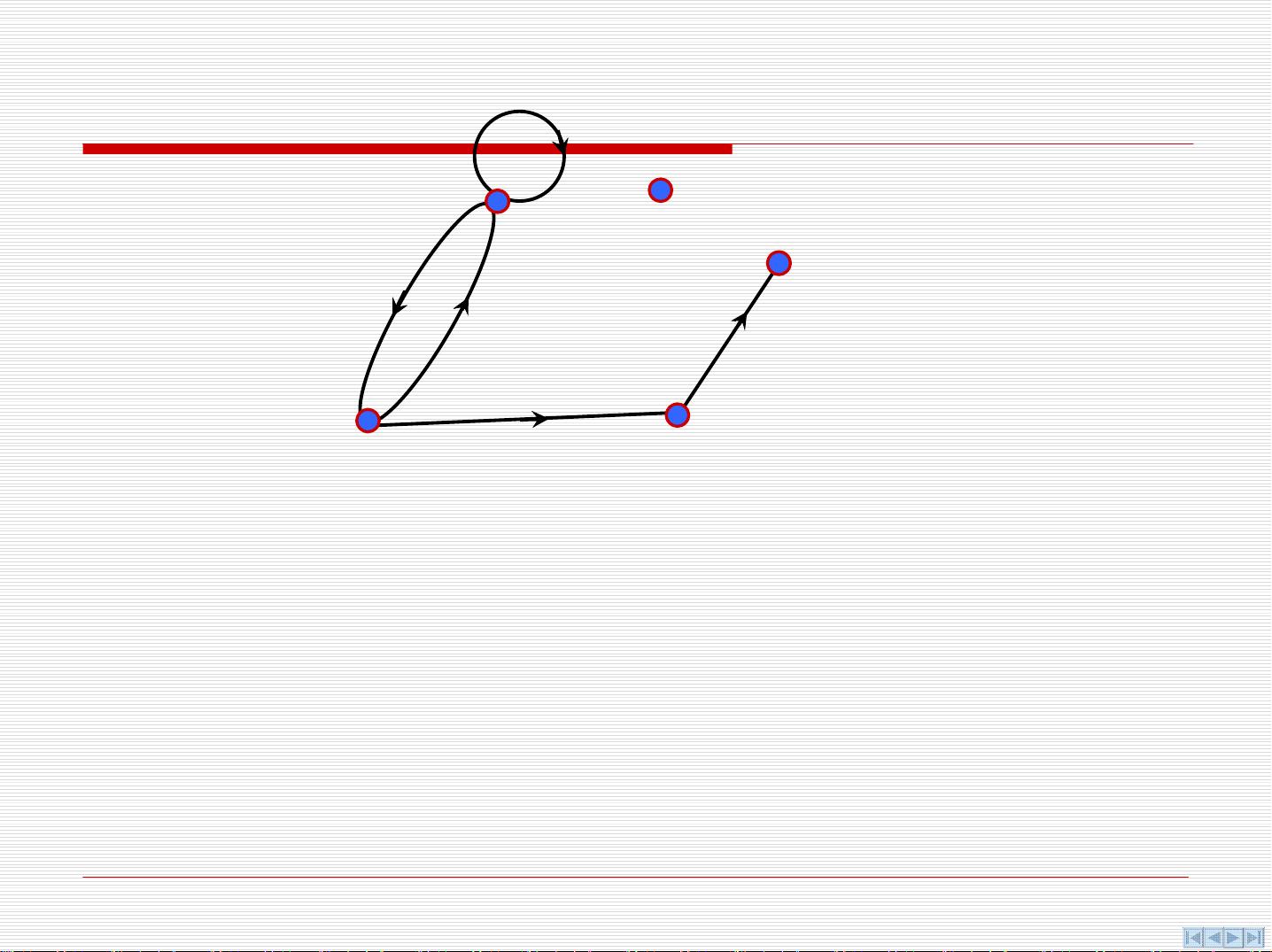
"哈尔滨工业大学的图论课程教材，主要涵盖了图论的基本概念、无向图与有向图、通路与回路、图的连通性、图的矩阵表示、最短路径及关键路径等内容。" 图论是离散数学的重要分支，起源于18世纪瑞士数学家欧拉解决的著名七桥问题。欧拉的工作标志着图论的诞生，并为后来的发展奠定了基础。在图论中，图形被用来表示事物间的关联，其中点代表实体，线则表示这些实体间的关系。图论的研究涵盖了许多领域，包括计算机科学、物理学、化学、运筹学、信息论、控制论以及社会经济等多个方面。 图论的基本概念包括无向图和有向图。无向图中的边是无序的，即任何两个顶点之间可以有一条或多条边，而这些边没有方向性。例如，如果V是顶点集，E是无序积V×V的多重子集，那么无向图G=<V,E>。有向图则不同，其边是有方向的，边的方向反映了从一个顶点到另一个顶点的关系。有向图D=<V,E>的E是V的卡氏积的多重子集，其中的元素称为有向边。 在图论中，研究的关键问题之一是图的连通性，这涉及到图中的通路和回路。通路是指从一个顶点到另一个顶点的一系列连续边，而回路则是从一个顶点出发并最终返回该顶点的通路。图的连通性分析对于理解网络结构和设计算法至关重要。 此外，图的矩阵表示是图论中另一重要概念，如邻接矩阵和度矩阵，它们提供了图形数据结构的抽象，便于进行数学分析和计算。例如，邻接矩阵可以表示图中每个顶点与其他顶点是否有边相连，而度矩阵则记录了每个顶点的度数，即与其相连的边的数量。 最短路径和关键路径问题在图论中占有重要地位。最短路径问题寻找的是两个顶点间路径长度最小的路径，广泛应用于网络优化和路由选择。关键路径则在项目管理中尤为重要，它确定了完成项目所需时间最长的依赖路径。 图论是通过图形模型来研究复杂系统关系的数学工具，其理论和应用广泛且深入。随着计算机科学和信息技术的发展，图论在算法设计、数据结构、网络分析等方面的作用愈发显著，成为解决实际问题不可或缺的理论基础。