MATLAB实现椭圆滤波器设计与仿真

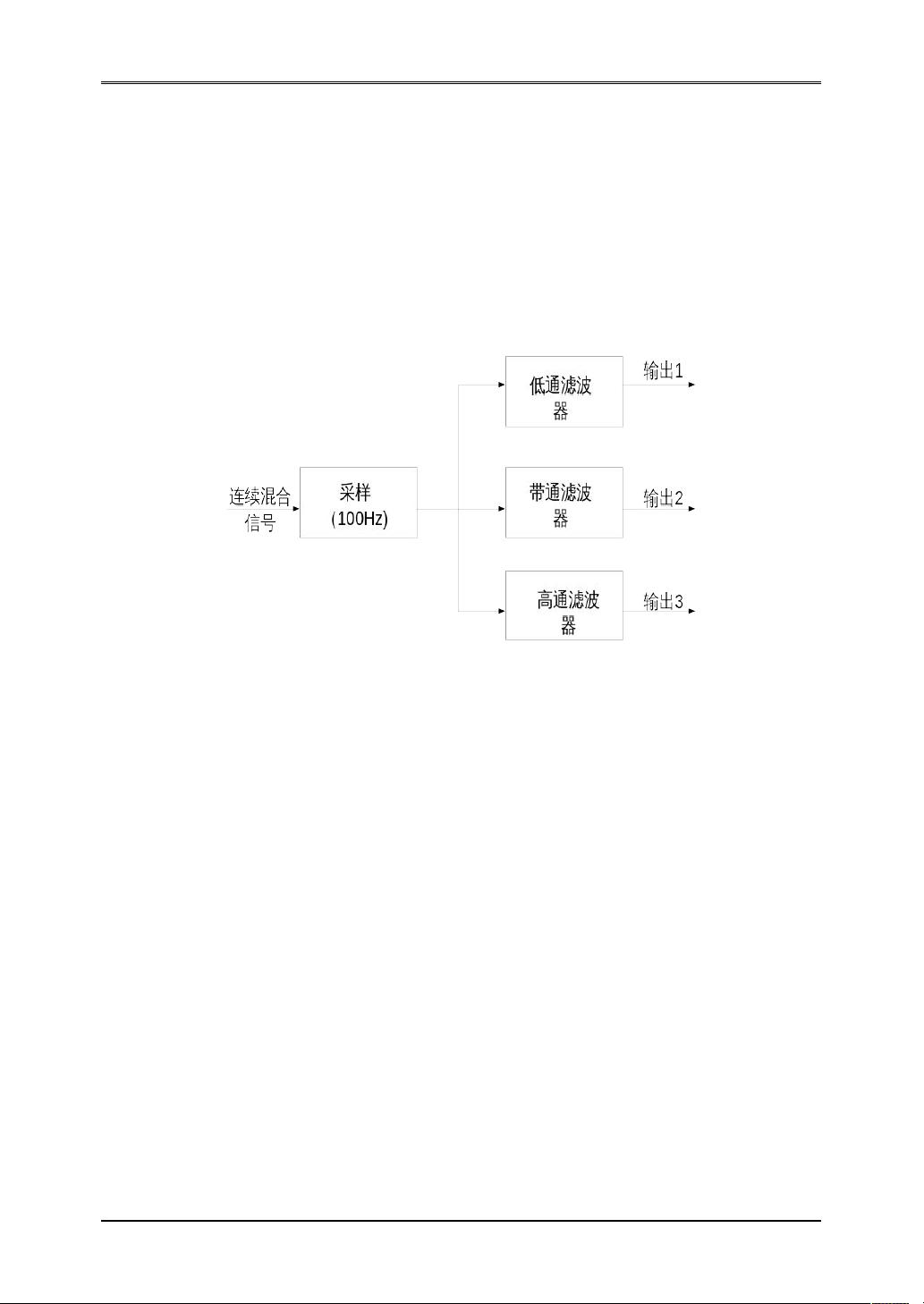
"椭圆滤波器的设计" 椭圆滤波器是一种在电子工程、应用数学和计算机科学中广泛使用的滤波器类型，也被称为考尔滤波器。这种滤波器以其独特的特性，即在通带和阻带内都具有等波纹的幅值响应而著称。椭圆滤波器的设计目标是通过牺牲通带和阻带的波动来换取更加陡峭的过渡带，从而在相同阶数下提供最窄的过渡带宽。在很多实际应用中，例如音频信号处理、通信系统和测量设备，椭圆滤波器因其陡峭的边缘衰减和优良的频率选择性而受到青睐。 设计椭圆滤波器通常涉及到利用特定的设计工具和算法，如MATLAB中的滤波器设计函数。在设计过程中，首先要理解滤波器的基本原理，包括零点和极点的分布，以及它们如何影响滤波器的频率响应。椭圆滤波器的幅度响应可以用雅可比椭圆函数RN(x)来描述，其中ε是一个关键参数，与通带的衰减程度相关。 在MATLAB环境中，设计低通、带通和高通椭圆滤波器的步骤通常包括以下几个阶段： 1. 定义滤波器参数：这包括设定通带和阻带边界、通带和阻带的允许波动、以及滤波器的阶数。 2. 计算滤波器系数：使用MATLAB的滤波器设计工具，如`ellip`函数，可以计算出滤波器所需的系数。 3. 生成滤波器结构：根据计算出的系数构建滤波器的零点和极点配置。 4. 信号采样与仿真：生成一个包含不同频率成分的信号，对其进行采样，然后应用设计好的滤波器进行滤波处理。 5. 频谱分析与结果评估：分析滤波后的信号频谱，检查滤波器的性能是否满足设计要求。 在实际应用中，椭圆滤波器常常用于去除信号中的谐波干扰，提高模拟信号的精度。例如，在声卡的语音合成输出或者实验室的信号发生器中，都可以看到椭圆滤波器的身影。由于其独特的性能优势，椭圆滤波器在众多领域都有广泛的应用。 总结起来，椭圆滤波器的设计是一项结合了理论知识和实践操作的技术。通过MATLAB等工具，我们可以有效地实现椭圆滤波器的设计，优化其性能，并在各种信号处理任务中利用其优势。对于工程师和研究人员来说，理解和掌握椭圆滤波器的基本原理和设计方法是至关重要的。