探索小波变换的时空解析：一种高级多媒体教程

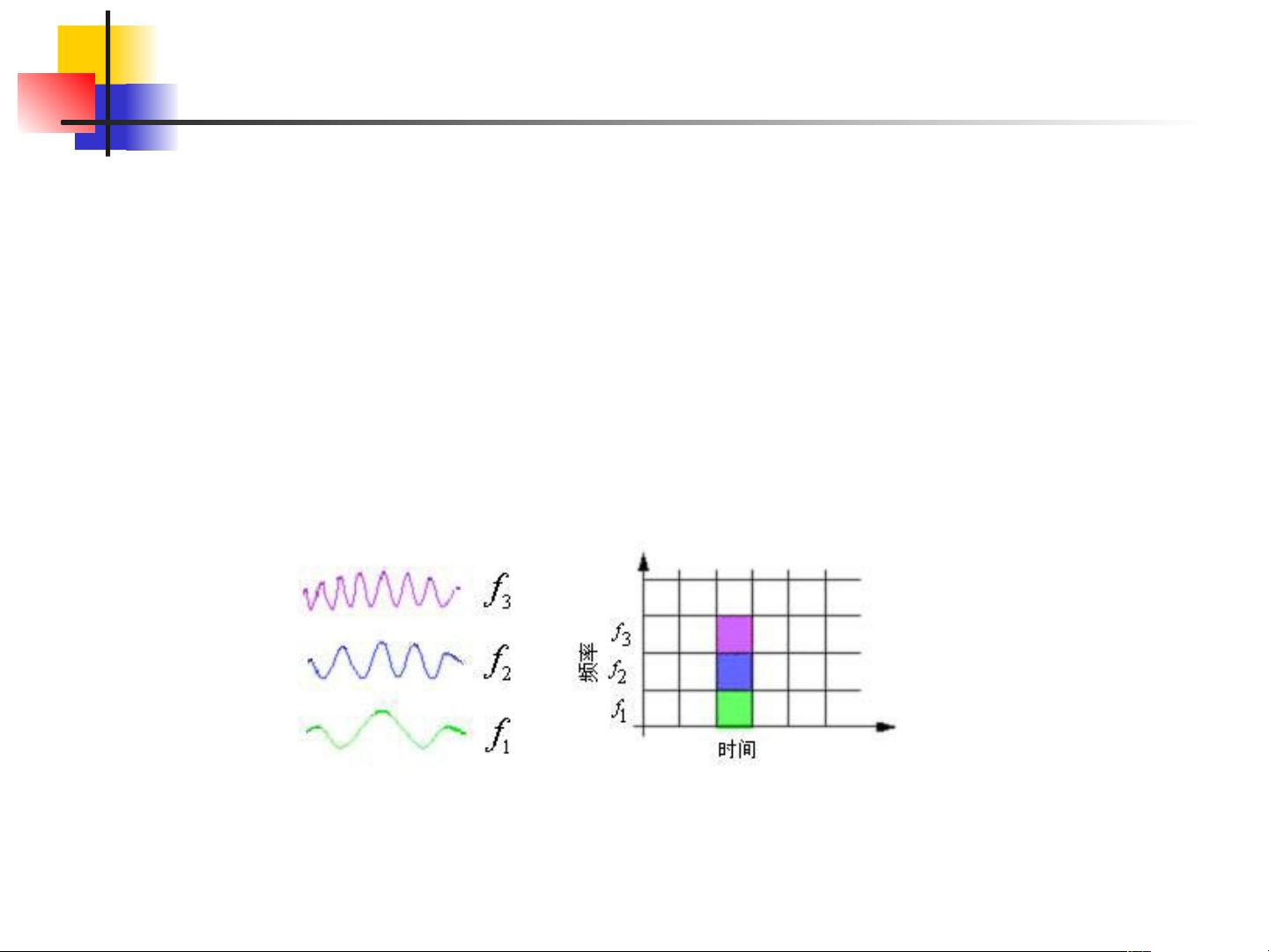
小波变换是一门重要的信号处理技术，尤其在音频、图像和视频等多媒体领域展现出了卓越的局部时频分析能力。它不同于传统的傅里叶变换，后者主要提供频率分辨率，但缺乏精确的时间定位。小波变换通过使用特定的数学函数，即小波，来克服这一局限性。 小波是一种特殊的数学函数，它在有限时间内变化，具有有限的持续时间和突发的频率和振幅特性，使得它能够在局部范围内捕捉信号的变化。这个概念起源于19世纪的傅立叶理论，该理论提出任何信号都可以表示为正弦和余弦函数的线性组合。然而，傅立叶变换在表示信号的时间信息上有所欠缺。 1984年，Grossmann和Morlet开发了Moret小波函数，而Daubechies则进一步提出了db6缩放函数和db6小波函数，这些是小波家族中的知名成员。小波可以分为全波和部分波，部分波如Moret小波和db6小波，是根据开发者的姓名命名的，它们各自具有独特的性质和应用。 哈尔函数是小波变换的基础，包括哈尔基函数和哈尔小波函数。哈尔基函数是构建小波的基本单元，而哈尔小波函数则通过尺度和移位操作进行调整，以适应不同频率和时间分辨率的需求。为了确保函数的规范化，需要考虑函数的幅度和相位特性，以及它们的数学结构。 哈尔小波变换是小波分析的核心部分，它通过结合尺度和移位操作，实现对信号在不同尺度和时间上的精细分析。这种变换允许我们同时获得信号在时间和频率域的信息，从而提供更为精确的信号特征描述。规范化算法则是确保变换结果的稳定性及可比性的重要步骤。 二维哈尔小波变换是对多维度信号进行分析的方法，它扩展了一维小波变换的概念，可用于处理图像等二维数据。二维小波变换可以通过实例演示来理解，如使用不同的小波和方法对图像进行分解和重构。这种方法在图像压缩、边缘检测、纹理分析等领域有着广泛应用。 小波变换是一门强大的工具，它弥补了傅立叶变换的不足，提供了更全面的信号分析视角。学习小波变换，对于那些已经熟悉傅立叶变换的读者来说，是一个自然的进阶，可以帮助他们理解和处理更加复杂的数据。通过深入了解哈尔函数、哈尔小波、规范化和二维变换，研究者和工程师可以充分利用小波变换的优势，在多媒体处理和信号分析中取得突破。