理解ARIMA模型：时间序列预测的关键

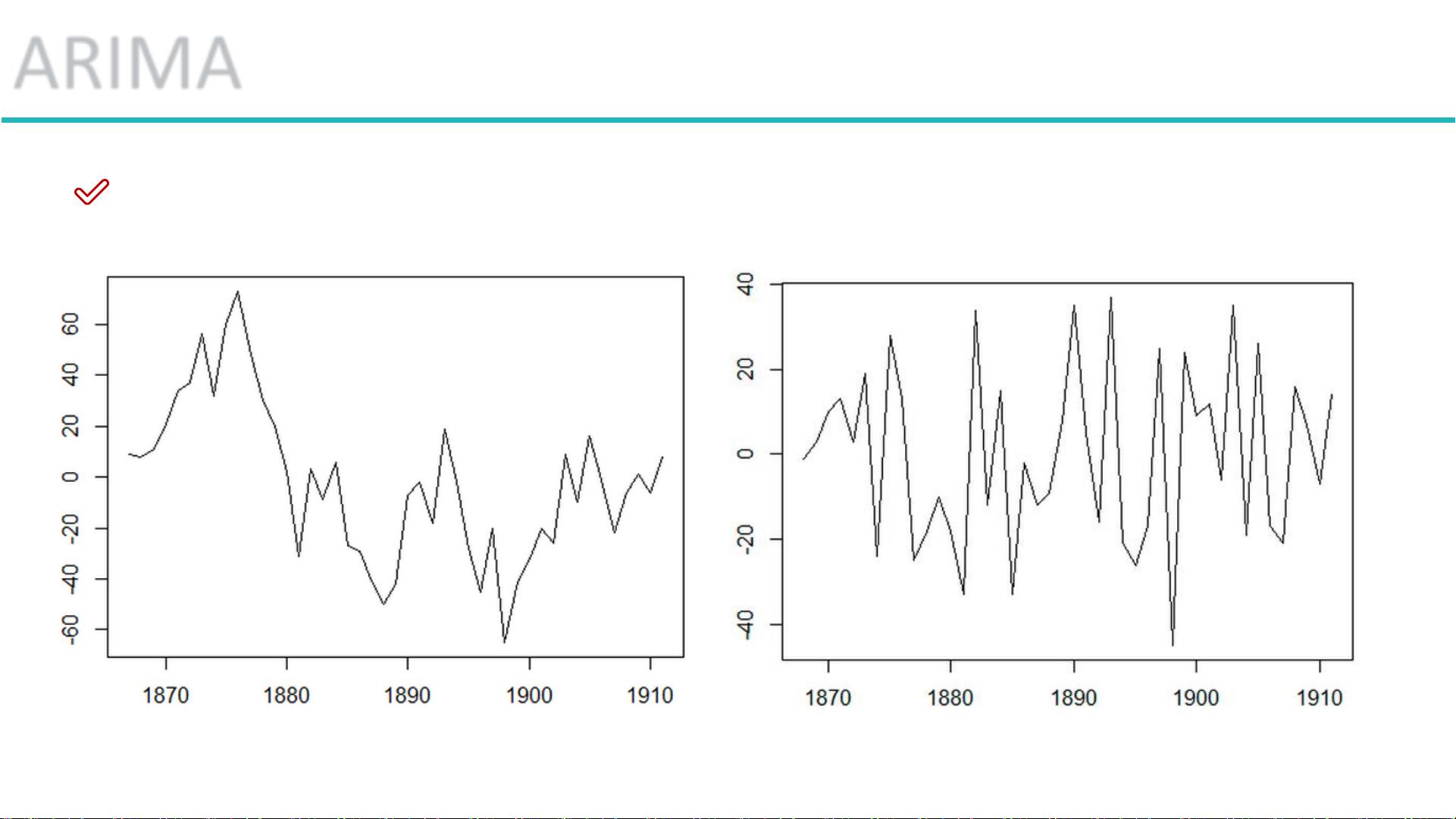
"时间序列分析--.pdf" 时间序列分析是一种统计方法，专门用于分析按时间顺序排列的数据序列。在该领域中，ARIMA模型（自回归整合移动平均模型）是一个核心概念，广泛应用于预测和建模具有时间依赖性的数据。 ARIMA模型是由三部分组成的：自回归（AR）、差分（I，即Integration）和移动平均（MA）。在深入理解ARIMA之前，我们需要了解平稳性这一关键概念。平稳性是指时间序列的统计特性（如均值和方差）保持不变，随着时间的推移，序列的形态不会发生显著变化。这在预测模型中很重要，因为平稳的时间序列使得预测未来值变得更加可靠。 严平稳和弱平稳是两种不同的平稳性类型。严平稳要求序列的概率分布不会随时间的平移而改变，例如白噪声，其期望始终为0，方差恒定为1。而弱平稳则关注序列的均值和相关系数保持不变，即使序列本身可能有波动，但其长期行为是可预测的。 在处理非平稳时间序列时，差分方法常常被用来使数据达到平稳状态。一阶差分是将序列在相邻时间点的差值作为新的观测值，以此减少趋势或季节性的影响。 自回归模型（AR）是ARIMA的一部分，它考虑了当前值与历史值之间的关系，用时间序列自身的历史数据来预测其未来值。AR模型必须基于平稳的时间序列，并遵循特定的数学形式，如p阶自回归过程，其中p是自回归项的阶数，φi是自相关系数。 移动平均模型（MA）则关注AR模型中误差项的累加，通过消除随机波动来提高预测精度。q阶移动平均模型定义了误差项如何与过去的误差项相结合来影响当前值。 自回归移动平均模型（ARMA）结合了自回归和移动平均的特性，形成一个更强大的工具，可以捕捉到时间序列中的复杂模式。ARIMA模型进一步扩展了ARMA模型，引入了差分操作（I），能够处理非平稳时间序列，通过差分将非平稳序列转化为平稳序列，然后用AR和MA部分进行建模。 自相关函数（ACF）和偏自相关函数（PACF）是识别ARIMA模型参数的关键工具。ACF测量了序列中任意两个时间点之间的相关性，而PACF则揭示了序列当前值与滞后值间直接的关系，排除了中间变量的影响。这两个函数在确定自回归阶数p和移动平均阶数q时起到至关重要的作用。 在应用ARIMA模型时，需要注意几个限制条件，比如自回归模型必须基于平稳序列，自相关系数需要适中，且模型适用于预测与前期值相关的现象。此外，移动平均模型通常用于消除随机波动，但不适用于所有情况。 时间序列分析和ARIMA模型提供了一套系统的方法来理解和预测随时间变化的数据，它们在经济学、金融、气象学、工程等多个领域都有广泛应用。正确理解和应用这些概念和方法，可以帮助我们更好地预测未来趋势，做出数据驱动的决策。