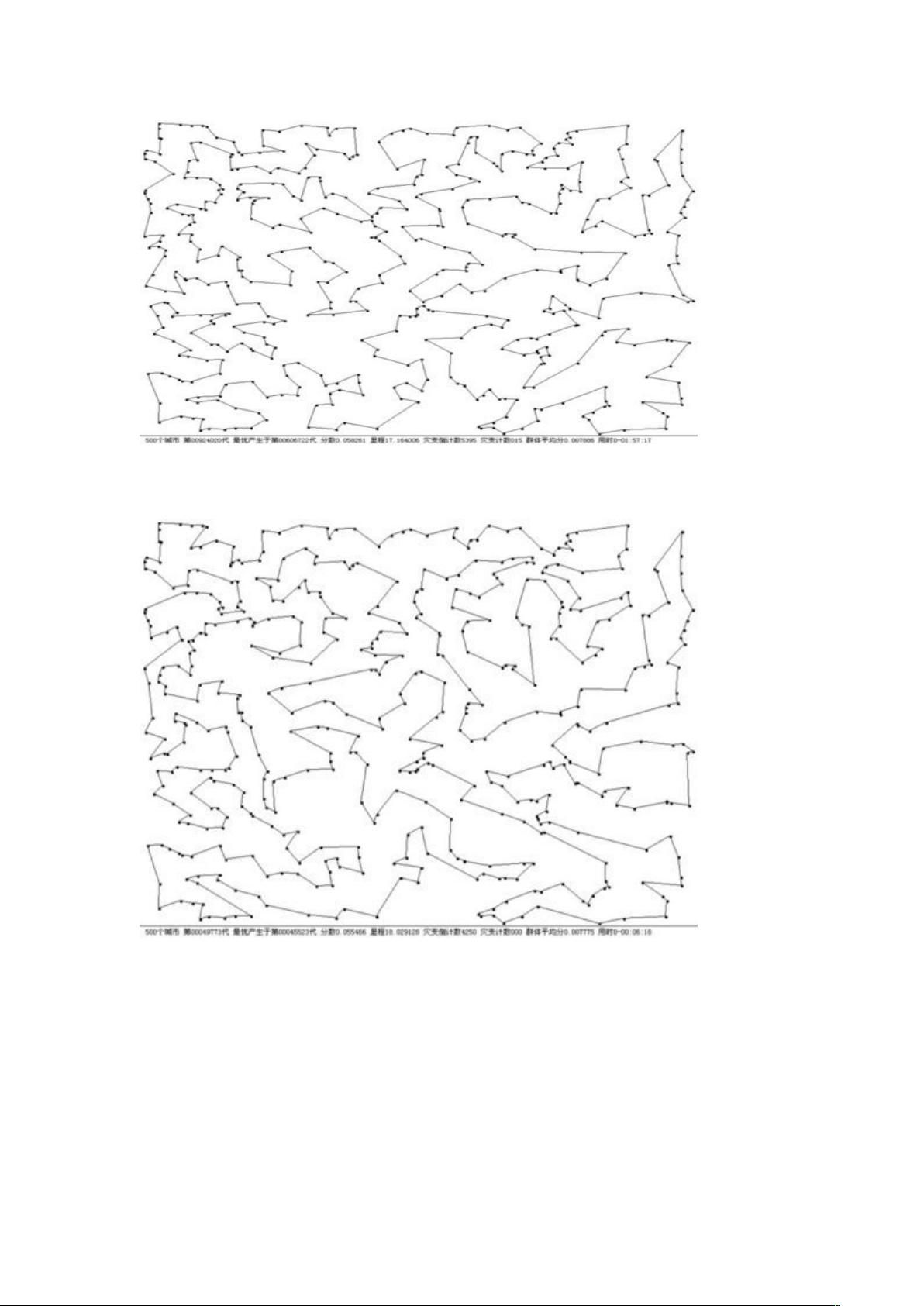
遗传算法求解旅行商问题详解及代码分享

"遗传算法解决TSP问题，遗传算法原理及应用" 遗传算法（Genetic Algorithm，GA）是一种模拟自然选择和遗传机制的全局优化算法，最初由John Holland提出。在旅行商问题（Traveling Salesman Problem, TSP）中，遗传算法常被用来寻找最短的可能路线，使得旅行商能访问给定城市一次并返回原点。TSP是一个经典的组合优化问题，具有NP完全性，传统的方法如贪心算法或动态规划往往难以找到最优解。 遗传算法的核心思想是模拟生物进化的过程，包括选择（Selection）、交叉（Crossover）和变异（Mutation）等操作。首先，通过随机初始化一个种群，每个个体代表一种可能的解决方案（在TSP中，即旅行路线）。然后，算法根据适应度函数（Fitness Function）评价每个个体的质量，适应度通常与解的质量（如路线长度）成反比。接下来，按照一定的概率，优秀个体（高适应度）更有可能被选中参与繁殖，即交叉操作，生成新的后代。同时，为了保持种群的多样性，还会进行变异操作，随机改变部分个体的部分特性。 在TSP问题中，选择操作通常是基于轮盘赌选择法，适应度高的个体有更大的机会被选中。交叉操作如单点交叉、多点交叉等，会选取一个随机点将两个父代个体的路线部分交换。变异操作则是在某个个体的路径上随机选择一个城市，将其移动到路径的另一个随机位置。 然而，遗传算法面临的主要挑战之一是避免陷入局部最优。描述中提到，单纯增加变异概率并不能有效解决问题，因为这可能导致算法变成随机搜索。为了避免局部最优，灾变策略被引入。灾变是指在一定条件下，清除当前种群中的所有优秀个体，迫使算法探索新的解决方案空间。灾变的触发时机可以设置为一定的迭代次数或者当种群多样性下降到一定程度时。 灾变倒计数方法就是其中一种实现方式，从一个初始值开始，每经过一代就减少计数值，当计数值归零时执行灾变。这种方法能够确保在算法运行一段时间后强制探索新的解空间，从而跳出局部最优。 遗传算法在解决TSP问题时，通过模拟生物进化过程，结合选择、交叉和变异操作，以及灾变策略，能够在全球范围内搜索可能的解决方案。然而，算法的性能和收敛速度依赖于参数的设定，如种群大小、交叉概率、变异概率和灾变频率等，这些都需要根据具体问题进行调整和优化。