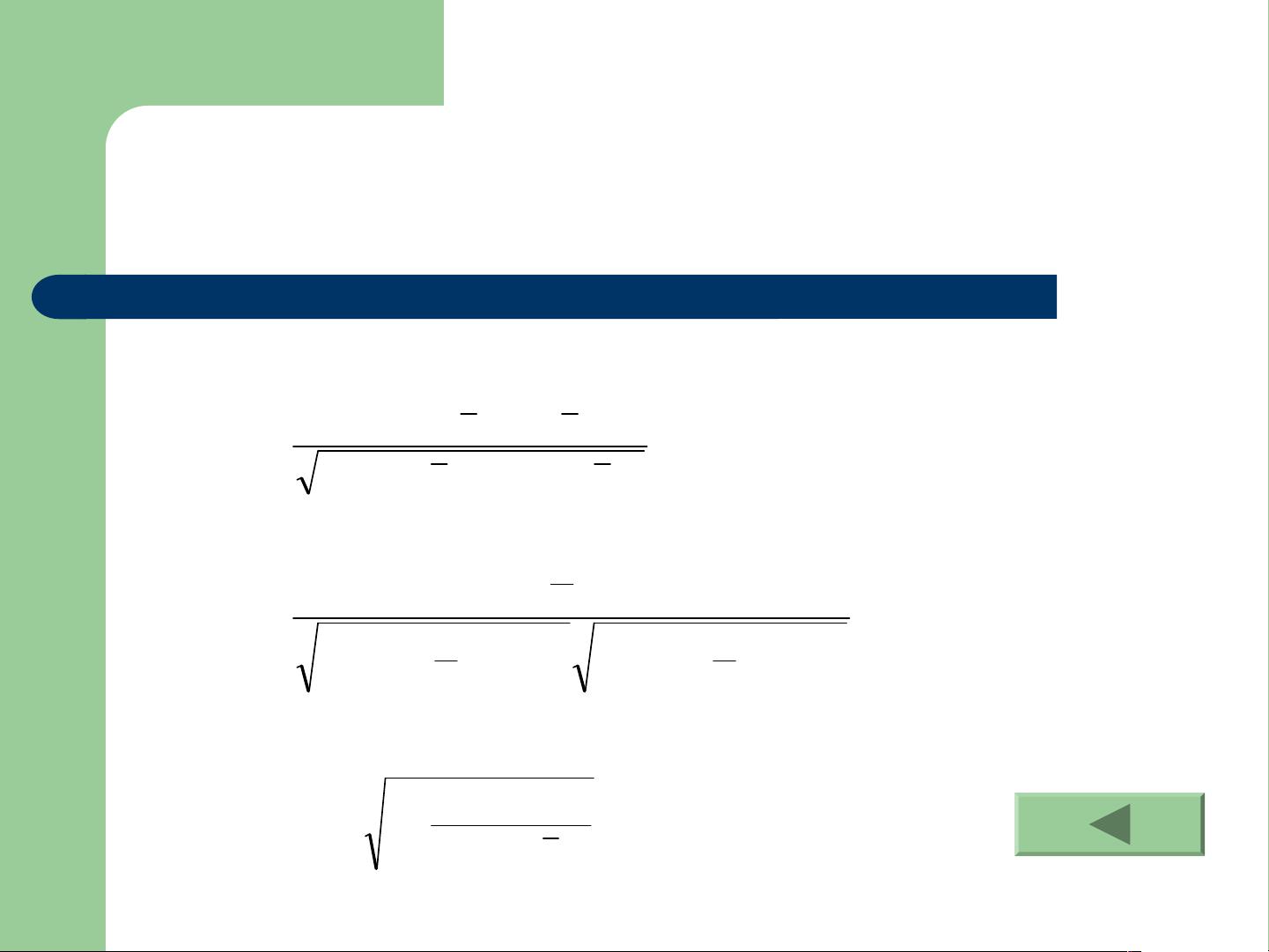
回归预测方法详解：从一元到多元线性与非线性

"市场调查与预测 第9章 回归预测.ppt" 回归预测是市场调查与预测中的一种重要技术，主要应用于根据已知数据预测未来趋势。它基于因果关系，通过统计方法寻找最佳的回归模型，以预测市场的变化。在回归预测中，预测的目标变量被称为因变量，而影响目标变量的变量称为自变量。 回归分析根据涉及的自变量数量，可分为一元回归、二元回归和多元回归。一元回归分析涉及一个因变量和一个自变量，二元回归分析涉及两个自变量，而多元回归则处理两个以上自变量的情况。此外，根据关系的线性与否，回归分析又可分为线性回归和非线性回归。 进行回归预测时，一般遵循以下步骤： 1. 判断因变量和自变量之间是否存在相关性，通常通过散点图初步观察。 2. 确定因变量与自变量的关系，即选择哪些变量对预测目标有显著影响。 3. 建立回归预测模型，例如对于一元线性回归，会形成一个简单的直线方程形式：y = a + bx，其中y是因变量，x是自变量，a是截距，b是斜率。 4. 对模型进行统计检验，如相关系数检验和t检验，以验证模型的有效性和参数的显著性。 5. 利用建立的模型进行预测，并评估预测结果的可信度，例如计算置信区间。 相关系数r是衡量两个变量间线性相关程度的指标，其值在-1到1之间。若r接近1或-1，表示强正相关或强负相关；若r接近0，则表明两者关联性较弱。在进行回归模型检验时，相关系数有助于判断模型的拟合程度。 t检验则用于检验回归参数a和b是否有统计学意义。如果t统计量的值在特定的显著性水平下落在拒绝域内，那么我们可以认为回归参数的估计值与零假设（无效应）显著不同，即该参数对模型的预测有显著贡献。 回归预测是一种强大的工具，用于分析变量间的复杂关系并进行预测。在营销领域，它可以用来预测销售趋势、消费者行为以及市场响应等，帮助企业制定更精准的市场策略。通过对历史数据的深入分析，回归模型可以帮助企业识别关键影响因素，从而做出更准确的决策。