分支定界法在Matlab中的实现与应用解析

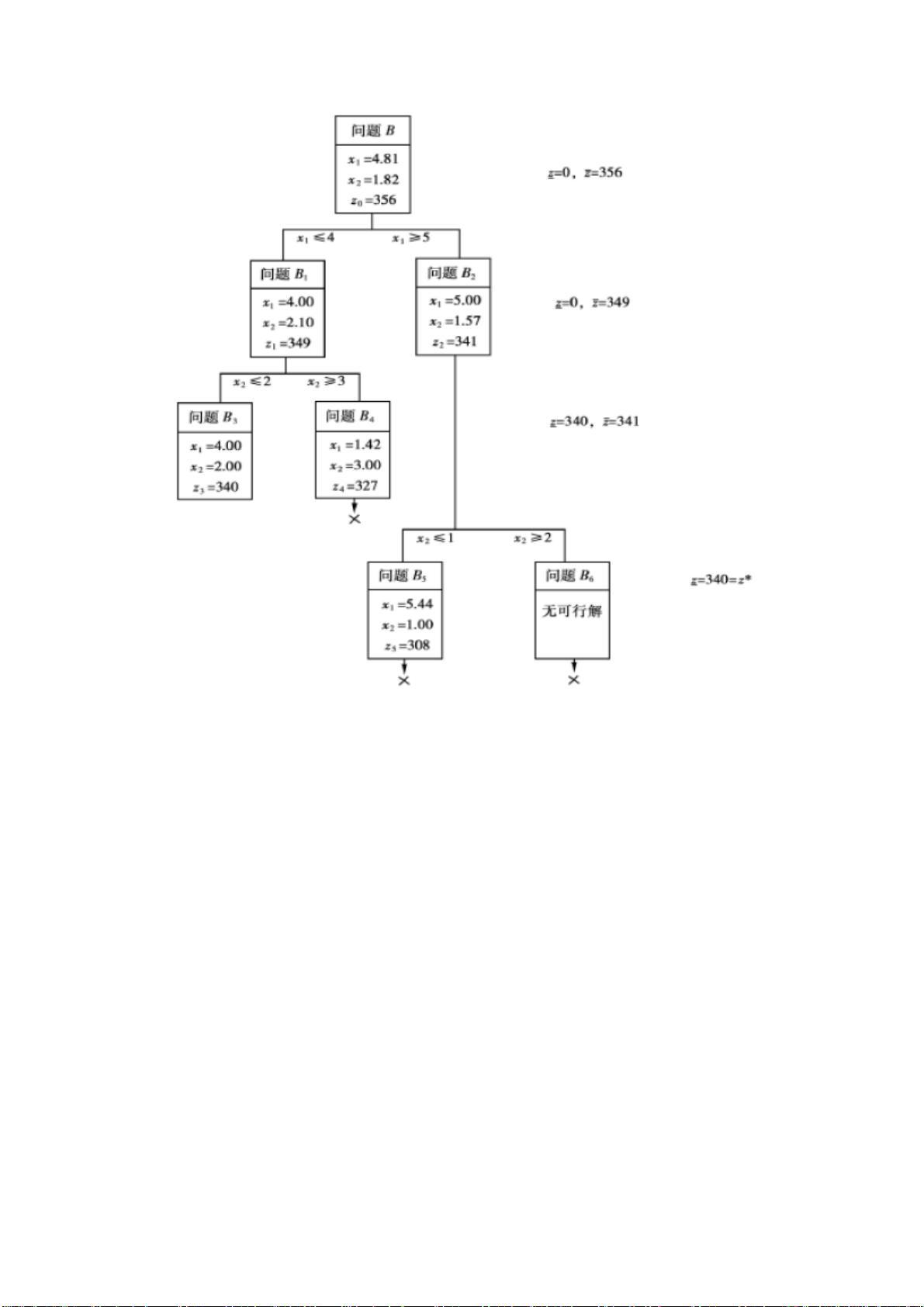
"该文档详细介绍了分支定界法在Matlab环境下的程序实现与验证，包括整数规划问题的基本概念，分支定界法的运算逻辑，程序设计逻辑框图，以及具体的Matlab函数jBranchBound的源代码和应用实例。此外，还提到了Matlab内置的整数线性规划求解函数intlinprog的使用方法。" 正文: 整数规划问题是在线性规划的基础上引入了变量必须取整数值的约束，这在实际应用中非常常见，如设备数量、人员配置等问题。当最优解为非整数时，简单的四舍五入处理可能无法得到可行解或最优解，因此需要专门的整数规划方法来解决。 分支定界法是一种有效求解整数规划问题的算法，其核心思想是将问题的可行域逐步分割为更小的子区域（分支），并在此过程中不断更新解的下界和上界，直到找到全局最优解或者确定无解。在描述分支定界法的运算逻辑时，文档可能会详细阐述如何选择分支节点、如何构造和剪枝子问题、如何维护搜索树以及如何更新边界。 Matlab程序jBranchBound是实现分支定界法的一个示例，提供了源代码供读者理解和学习。这个程序通常会包含初始化、分支策略、边界更新、回溯和剪枝等关键部分。文档中列举了多个实例，如单变量和多变量的整数规划问题，以及0-1整数规划问题，通过这些例子，读者可以直观地看到如何运用该程序解决实际问题。 此外，Matlab自2014版起内置了intlinprog函数，这是一个用于求解混合整数线性规划问题的工具。文档介绍了intlinprog的调用格式和使用方法，通过示例展示了如何利用此函数求解整数规划问题，这对于不熟悉分支定界法或希望快速解决整数规划问题的用户非常实用。 这篇文档不仅深入讲解了整数规划问题和分支定界法，还提供了实际的Matlab编程实现，旨在帮助读者更好地理解和应用这些理论知识。对于学习优化算法和Matlab编程的读者来说，这是一份非常有价值的学习资料。