ns-3 LTE 模型设计与文档详解

需积分: 15 133 浏览量更新于2024-07-21 收藏 6.64MB PDF 举报

NS-3 Model Library for LTE Simulation NS-3是一个广泛使用的开源仿真平台，特别适用于研究和开发无线通信系统，包括长期演进（LTE）技术。该文档是关于NS-3 LTE模块的详细设计、用户指南、测试、性能分析以及引用资料的综合资源，针对的是ns-3-dev版本，发布日期为2015年4月6日。 19.1 设计文档设计文档提供了对LTE-EPC（演进分组核心网）模拟模型的全面概述。模型的核心结构分为两个主要组件： - **LTE模型**：这部分涵盖了从物理层（PHY）到应用层的完整LTE无线协议栈，包括RRC（Radio Resource Control）、PDCP（Packet Data Convergence Protocol）、RLC（Random Access Channel）、MAC（Medium Access Control）等。这些实体完全位于UE（用户设备）和eNB（执行基站）节点内部，模拟了实际网络中的无线传输过程。 - **EPC模型**：这个部分关注核心网络的接口、协议和实体，如MME（ Mobility Management Entity）、SGW（ Serving Gateway）、PGW（ Packet Data Network Gateway）等，它们负责处理用户数据传输、会话管理和服务计费等功能，构成了连接UE与无线接入网之间的桥梁。文档形式多样，包括： - ns-3 Doxygen：提供了对ns-3模拟器公共API的详尽文档，帮助开发者理解和使用这些接口。 - 最新版本的教程、手册和模型库文档，如本篇文档，为用户提供易于理解的指导，包括LTE模块的安装、配置和使用方法。 - ns-3 wiki：在线社区资源，包含实时更新的项目信息、教程和解决方案，方便用户交流和协作。整个文档采用reStructuredText格式，并存储在ns-3源代码的doc/models目录下，便于开发者获取和维护。通过阅读这份文档，用户可以深入了解NS-3如何模拟LTE网络，以及如何进行有效的模型设置和性能评估。这对于研究者、开发者和教育工作者来说，是一个极其宝贵的工具，能够促进对下一代移动通信技术的理解和研究。

ns-3 Model Library, Release ns-3-dev

MAC to Channel delay

To model the latency of real MAC and PHY implementations, the PHY model simulates a MAC-to-channel delay in

multiples of TTIs (1ms). The transmission of both data and control packets are delayed by this amount.

CQI feedback

The generation of CQI feedback is done accordingly to what speciﬁed in [FFAPI]. In detail, we considered the gener-

ation of periodic wideband CQI (i.e., a single value of channel state that is deemed representative of all RBs in use)

and inband CQIs (i.e., a set of value representing the channel state for each RB).

The CQI index to be reported is obtained by ﬁrst obtaining a SINR measurement and then passing this SINR measure-

ment the Adaptive Modulation and Coding which will map it to the CQI index.

In downlink, the SINR used to generate CQI feedback can be calculated in two different ways:

1. Ctrl method: SINR is calculated combining the signal power from the reference signals (which in the simulation

is equivalent to the PDCCH) and the interference power from the PDCCH. This approach results in consider-

ing any neighboring eNB as an interferer, regardless of whether this eNB is actually performing any PDSCH

transmission, and regardless of the power and RBs used for eventual interfering PDSCH transmissions.

2. Mixed method: SINR is calculated combining the signal power from the reference signals (which in the sim-

ulation is equivalent to the PDCCH) and the interference power from the PDSCH. This approach results in

considering as interferers only those neighboring eNBs that are actively transmitting data on the PDSCH, and

allows to generate inband CQIs that account for different amounts of interference on different RBs according

to the actual interference level. In the case that no PDSCH transmission is performed by any eNB, this method

consider that interference is zero, i.e., the SINR will be calculated as the ratio of signal to noise only.

To switch between this two CQI generation approaches, LteHelper::UsePdschForCqiGeneration needs to

be conﬁgured: false for ﬁrst approach and true for second approach (true is default value):

Config::SetDefault ("ns3::LteHelper::UsePdschForCqiGeneration", BooleanValue (true));

In uplink, two types of CQIs are implemented:

• SRS based, periodically sent by the UEs.

• PUSCH based, calculated from the actual transmitted data.

The scheduler interface include an attribute system calld UlCqiFilter for managing the ﬁltering of the CQIs

according to their nature, in detail:

• SRS_UL_CQI for storing only SRS based CQIs.

• PUSCH_UL_CQI for storing only PUSCH based CQIs.

• ALL_UL_CQI for storing all the CQIs received.

It has to be noted that, the FfMacScheduler provides only the interface and it is matter of the actual scheduler

implementation to include the code for managing these attibutes (see scheduler related section for more information

on this matter).

Interference Model

The PHY model is based on the well-known Gaussian interference models, according to which the powers of interfer-

ing signals (in linear units) are summed up together to determine the overall interference power.

The sequence diagram of Figure Sequence diagram of the PHY interference calculation procedure shows how inter-

fering signals are processed to calculate the SINR, and how SINR is then used for the generation of CQI feedback.

19.1. Design Documentation 157

ns-3 Model Library, Release ns-3-dev

LTE Spectrum Model

The usage of the radio spectrum by eNBs and UEs in LTE is described in [TS36101]. In the simulator, radio spectrum

usage is modeled as follows. Let f

denote the LTE Absolute Radio Frequency Channel Number, which identiﬁes the

carrier frequency on a 100 kHz raster; furthermore, let B be the Transmission Bandwidth Conﬁguration in number of

Resource Blocks. For every pair (f

, B) used in the simulation we deﬁne a corresponding SpectrumModel using the

functionality provided by the Spectrum Module . model using the Spectrum framework described in [Baldo2009]. f

and B can be conﬁgured for every eNB instantiated in the simulation; hence, each eNB can use a different spectrum

model. Every UE will automatically use the spectrum model of the eNB it is attached to. Using the MultiModelSpec-

trumChannel described in [Baldo2009], the interference among eNBs that use different spectrum models is properly

accounted for. This allows to simulate dynamic spectrum access policies, such as for example the spectrum licensing

policies that are discussed in [Ofcom2600MHz].

Data PHY Error Model

The simulator includes an error model of the data plane (i.e., PDSCH and PUSCH) according to the standard link-

to-system mapping (LSM) techniques. The choice is aligned with the standard system simulation methodology of

OFDMA radio transmission technology. Thanks to LSM we are able to maintain a good level of accuracy and at the

same time limiting the computational complexity increase. It is based on the mapping of single link layer performance

obtained by means of link level simulators to system (in our case network) simulators. In particular link the layer

simulator is used for generating the performance of a single link from a PHY layer perspective, usually in terms

of code block error rate (BLER), under speciﬁc static conditions. LSM allows the usage of these parameters in

more complex scenarios, typical of system/network simulators, where we have more links, interference and “colored”

channel propagation phenomena (e.g., frequency selective fading).

To do this the Vienna LTE Simulator [ViennaLteSim] has been used for what concerns the extraction of link layer

performance and the Mutual Information Based Effective SINR (MIESM) as LSM mapping function using part of the

work recently published by the Signet Group of University of Padua [PaduaPEM].

MIESM

The speciﬁc LSM method adopted is the one based on the usage of a mutual information metric, commonly referred

to as the mutual information per per coded bit (MIB or MMIB when a mean of multiples MIBs is involved). Another

option would be represented by the Exponential ESM (EESM); however, recent studies demonstrate that MIESM

outperforms EESM in terms of accuracy [LozanoCost].

The mutual information (MI) is dependent on the constellation mapping and can be calculated per transport block (TB)

basis, by evaluating the MI over the symbols and the subcarrier. However, this would be too complex for a network

simulator. Hence, in our implementation a ﬂat channel response within the RB has been considered; therefore the

overall MI of a TB is calculated averaging the MI evaluated per each RB used in the TB. In detail, the implemented

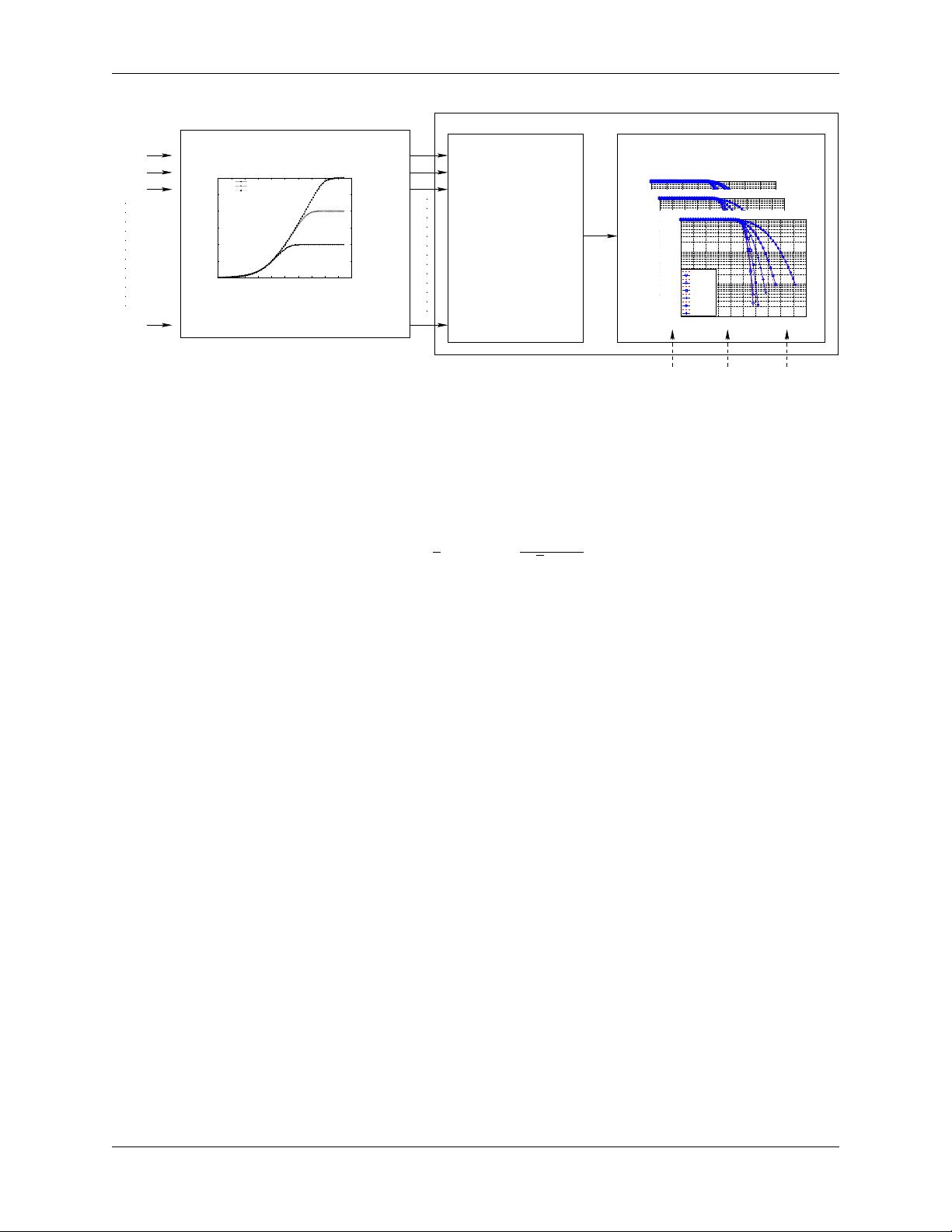
scheme is depicted in Figure MIESM computational procedure diagram, where we see that the model starts by evalu-

ating the MI value for each RB, represented in the ﬁgure by the SINR samples. Then the equivalent MI is evaluated

per TB basis by averaging the MI values. Finally, a further step has to be done since the link level simulator returns

the performance of the link in terms of block error rate (BLER) in a addive white guassian noise (AWGN) channel,

where the blocks are the code blocks (CBs) independently encoded/decoded by the turbo encoder. On this matter the

standard 3GPP segmentation scheme has been used for estimating the actual CB size (described in section 5.1.2 of

[TS36212]). This scheme divides the the TB in N

−

blocks of size K

−

and N

K+

blocks of size K

. Therefore the

overall TB BLER (TBLER) can be expressed as

T BLER = 1 −

i=1

(1 − CBLER

)

where the CBLER

is the BLER of the CB i obtained according to the link level simulator CB BLER curves. For

estimating the CBLER

, the MI evaluation has been implemented according to its numerical approximation deﬁned

19.1. Design Documentation 159

ns-3 Model Library, Release ns-3-dev

0 1 2 3 4 5 6 7 8

−3

−2

−1

SNR

BLER

TB = 6000 (AWGN)

TB = 6000 (estimated)

TB = 4000 (AWGN)

TB = 4000 (estimated)

TB = 2560 (AWGN)

TB = 2560 (estimated)

TB = 1024 (AWGN)

TB = 1024 (estimated)

TB = 512 (AWGN)

TB = 512 (estimated)

TB = 256 (AWGN)

TB = 256 (estimated)

TB = 160 (AWGN)

TB = 160 (estimated)

-20 -15 -10 -5 0 5 10 15 20 25 30

RBIR

Signal-to-noise ratio SNR [dB]

QPSK

16QAM

64QAM

4 4.5 5 5.5 6 6.5 7 7.5 8 8.5 9

−3

−2

−1

SNR

BLER

TB = 6000 (AWGN)

TB = 6000 (estimated)

TB = 4000 (AWGN)

TB = 4000 (estimated)

TB = 2560 (AWGN)

TB = 2560 (estimated)

TB = 1024 (AWGN)

TB = 1024 (estimated)

TB = 512 (AWGN)

TB = 512 (estimated)

TB = 256 (AWGN)

TB = 256 (estimated)

4 4.5 5 5.5 6 6.5 7 7.5 8 8.5 9

−3

−2

−1

SNR

BLER

TB = 6000 (AWGN)

TB = 6000 (estimated)

TB = 4000 (AWGN)

TB = 4000 (estimated)

TB = 2560 (AWGN)

TB = 2560 (estimated)

TB = 1024 (AWGN)

TB = 1024 (estimated)

TB = 512 (AWGN)

TB = 512 (estimated)

TB = 256 (AWGN)

TB = 256 (estimated)

SINR#1

SINR#2

SINR#3

SINR#N

I#1

I#2

I#3

Modulation Model

Information

collection & correction

MI−metric

TB length MCS ECR

Performance

(tables)

Coding Model

I#N

64QAM

Vienna LTE Simulator Mapping

16QAM

QPSK

SINR

RBIR

Figure 19.12: MIESM computational procedure diagram

in [wimaxEmd]. Moreover, for reducing the complexity of the computation, the approximation has been converted

into lookup tables. In detail, Gaussian cumulative model has been used for approximating the AWGN BLER curves

with three parameters which provides a close ﬁt to the standard AWGN performances, in formula:

CBLER



1 − erf



x − b

ECR

√

ECR



where x is the MI of the TB, b

ECR

represents the “transition center” and c

ECR

is related to the “transition width”

of the Gaussian cumulative distribution for each Effective Code Rate (ECR) which is the actual transmission rate

according to the channel coding and MCS. For limiting the computational complexity of the model we considered

only a subset of the possible ECRs in fact we would have potentially 5076 possible ECRs (i.e., 27 MCSs and 188 CB

sizes). On this respect, we will limit the CB sizes to some representative values (i.e., 40, 140, 160, 256, 512, 1024,

2048, 4032, 6144), while for the others the worst one approximating the real one will be used (i.e., the smaller CB

size value available respect to the real one). This choice is aligned to the typical performance of turbo codes, where

the CB size is not strongly impacting on the BLER. However, it is to be notes that for CB sizes lower than 1000 bits

the effect might be relevant (i.e., till 2 dB); therefore, we adopt this unbalanced sampling interval for having more

precision where it is necessary. This behaviour is conﬁrmed by the ﬁgures presented in the Annes Section.

BLER Curves

On this respect, we reused part of the curves obtained within [PaduaPEM]. In detail, we introduced the CB size depen-

dency to the CB BLER curves with the support of the developers of [PaduaPEM] and of the LTE Vienna Simulator.

In fact, the module released provides the link layer performance only for what concerns the MCSs (i.e, with a given

ﬁxed ECR). In detail the new error rate curves for each has been evaluated with a simulation campaign with the link

layer simulator for a single link with AWGN noise and for CB size of 104, 140, 256, 512, 1024, 2048, 4032 and

6144. These curves has been mapped with the Gaussian cumulative model formula presented above for obtaining the

correspondents b

ECR

and c

ECR

parameters.

The BLER perfomance of all MCS obtained with the link level simulator are plotted in the following ﬁgures (blue

lines) together with their correspondent mapping to the Gaussian cumulative distribution (red dashed lines).

Integration of the BLER curves in the ns-3 LTE module

The model implemented uses the curves for the LSM of the recently LTE PHY Error Model released in the ns3 com-

munity by the Signet Group [PaduaPEM] and the new ones generated for different CB sizes. The LteSpectrumPhy

160 Chapter 19. LTE Module

剩余170页未读，继续阅读

dianxinxiaozi2

粉丝: 0
资源: 2

ns-3 LTE 模型设计与文档详解

lena--NS3仿真lte项目

NS3.26模块库model library.pdf

ns-3 lte模块详细介绍文档

ns-3-model-library.pdf.zip_jumpi97_ns-3_tutorial

ns-3-model-library.pdf

lte.rar_c++ ns-2_ns-2 lte_ns2 lte_ns2 队列管理

matlab条纹代码-ns-3-validation:用于ns-3LTE模块的3GPP验证的文件

ns-3-manual、model-library、tutorial

ns-3-tutorial.pdf

ns-3-manual.pdf

最新资源