KMP算法解析：提升字符串模式匹配效率

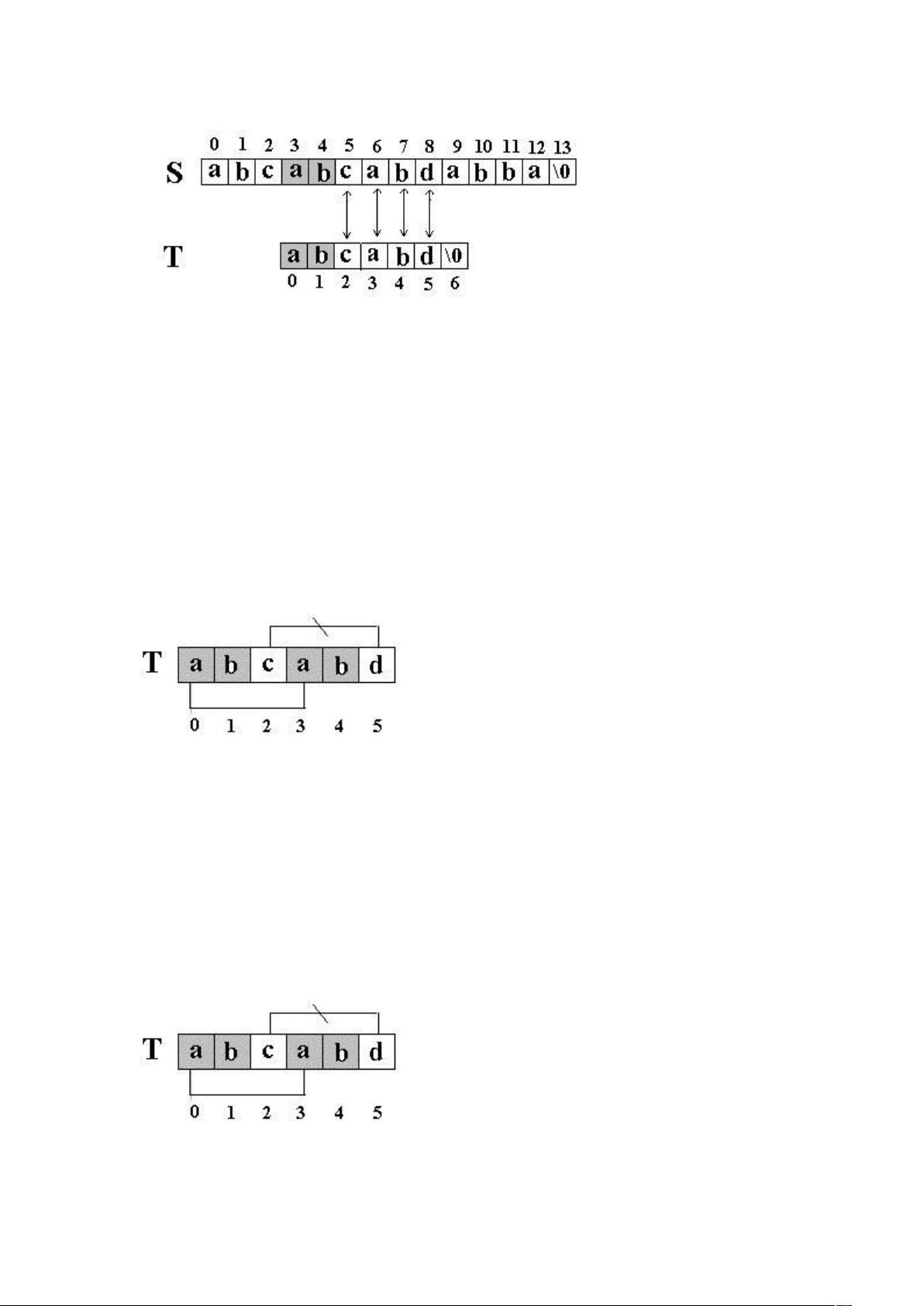
"KMP字符串模式匹配详解" KMP算法，全称为Knuth-Morris-Pratt算法，是一种在文本字符串中高效地查找模式串（目标字符串）的算法。相较于简单的暴力匹配方法，KMP算法避免了不必要的回溯，显著提高了搜索效率。其核心思想是利用模式串的已知信息来减少不必要的比较，尤其是在遇到不匹配的情况时。 在简单匹配算法中，当主串S和模式串T在某个位置比较不匹配时，算法会将模式串T回溯到起始位置，而主串S则向前移动一位，这种做法在模式串中存在重复字符序列时会引发大量的无效比较。例如，在查找"abcabd"于"abcabcabdabba"中的位置时，简单的匹配算法会在多个位置重复比较相同的字符序列，导致效率低下。 KMP算法通过构造一个部分匹配表（也称为“失配表”或“最长公共前后缀表”），来解决这个问题。这个表记录了在模式串T中每个位置的字符与之前字符组成的最长达子串的长度。当发生不匹配时，根据部分匹配表，可以直接确定模式串应向右移动多少位，而无需从头开始比较。 例如，对于模式串"abcabd"，部分匹配表可能如下： - T[0]: 0 - T[1]: 0 - T[2]: 1 (因为"a"和"ab"的公共前后缀长度为1) - T[3]: 2 (因为"bc"和"abc"的公共前后缀长度为2) - T[4]: 0 - T[5]: 1 (因为"d"和"abcab"没有公共前后缀，但与"abcabd"的后一个字符有公共前后缀) 在匹配过程中，如果在位置i处S[i]与T[j]不匹配，那么模式串T会根据部分匹配表向前移动j个位置，而不是回到起点。这样，KMP算法能够在大多数情况下避免了重复比较，从而提高效率。 在上述例子中，当第一次失配发生在S[5]和T[5]时，根据部分匹配表，T会回退到位置2，而S保持在当前位置6，继续比较。如此，KMP算法可以更有效地找到模式串在主串中的位置，时间复杂度为O(m+n)，其中m是主串S的长度，n是模式串T的长度。 总结来说，KMP算法通过部分匹配表优化了字符串匹配的过程，减少了不必要的比较次数，尤其在处理包含重复子串的模式时，效率远高于简单的暴力匹配。理解并实现KMP算法对于处理大量字符串数据的问题具有重要的实际意义。