MATLAB系统辨识工具箱详解：参数与非参数模型

"系统识别 matlab第6章 控制工程类工具箱介绍" MATLAB的控制工程类工具箱是专为自动控制领域的研究人员设计的一系列工具集合，它极大地扩展了MATLAB的功能，使得在符号计算、图形建模、数据处理以及硬件实时交互等方面的工作变得更加便捷。工具箱数量众多，涵盖自动控制、信号处理、图像处理等多个领域，每个工具箱都有配套的Help命令，用于获取函数用法信息，用户还可以根据实际需求定制自己的工具箱。 系统辨识工具箱是其中一个重要组成部分，主要用于通过实验数据来构建和分析动态系统的数学模型。这个工具箱的主要功能包括： 1. 参数模型辨识：支持ARX、ARMAX、BJ以及状态空间和输入误差等不同类型的模型辨识。 2. 非参数模型辨识：例如脉冲响应模型和频域描述模型，用于描述系统特性。 3. 模型验证：通过对比真实输出和模型预测数据的残差，评估模型的准确性。 4. 递推算法：用于ARX和ARMAX模型的在线辨识。 5. 建立和转换模型类的函数：提供了丰富的函数库，便于用户进行模型的构建和转换。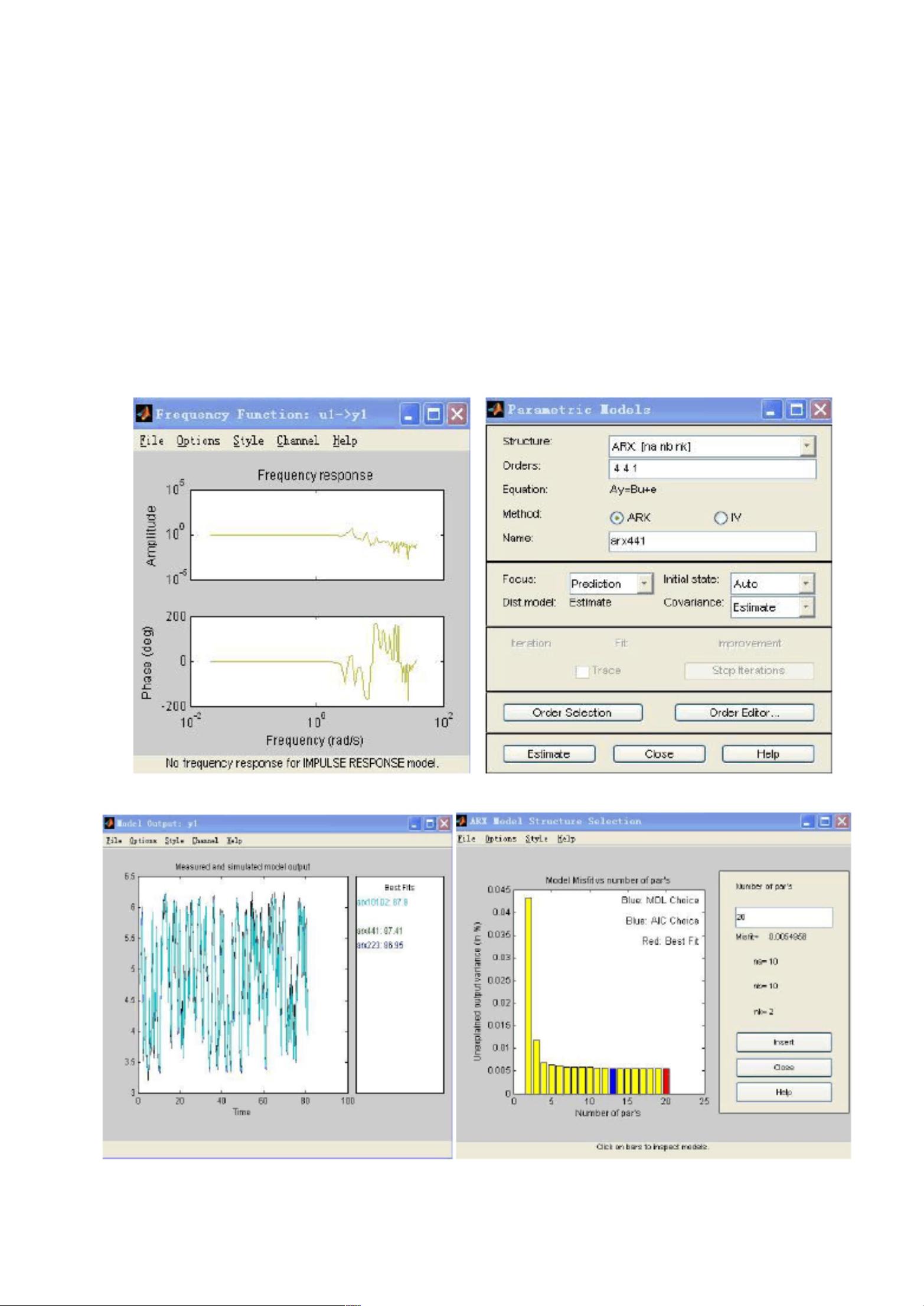 6. 图形用户界面：提供直观的交互式环境，支持模型选择、数据处理和估计等功能。 系统辨识的基本流程包括实验设计、模型结构辨识、模型参数辨识和模型检验。常见的参数模型类有： - ARX模型：输出y(t)是输入u(t)的线性函数，加上过去n个输出的累加，形式为A(q)y(t) = B(q)u(t-nk) + e(t)。 - ARMAX模型：在ARX模型基础上增加了误差项e(t)，形式为A(q)y(t) = B(q)u(t-nk) + C(q)e(t)。 - BJ模型（Box-Jenkins模型）：是ARX模型和误差项的组合，形式为y(t) = [B(q)/F(q)]u(t-nk) + [C(q)/D(q)]e(t)。 - 输入误差模型：与BJ模型类似，但误差项不包含输入的传递函数，形式为A(q)y(t) = [B(q)/F(q)]u(t-nk) + e(t)。 非参数模型，如脉冲响应模型，描述了输入u(t)对输出y(t)的影响，通过系统对单位阶跃响应的累积来表达系统特性。此外，频域描述模型则是在频域内对系统进行建模，适用于频率响应分析。 MATLAB的系统辨识工具箱为控制工程的研究和应用提供了强大的支持，它可以帮助用户从数据中提取出系统的动态行为，从而进行控制策略的设计和优化。