排序算法详解：冒泡、插入、选择、归并与快速排序

"这篇文档涵盖了第4章的算法知识，主要涉及了各种排序算法的总结，包括冒泡排序、插入排序、选择排序、快速排序、归并排序和堆排序，以及图上的最短路径算法如DFS、BFS、Dijkstra和Floyd算法，还有最小生成树的Kruskal和Prim算法，以及Hash概念。文档特别强调了这些算法的时间复杂度和稳定性，并提供了相关的链接以供深入学习。" 排序算法是计算机科学中非常基础且重要的概念，它们用于组织和优化数据处理。以下是对几种常见排序算法的详细解释： 1. 冒泡排序：通过重复遍历待排序的列表，比较相邻元素并交换位置来排序。冒泡排序在最好情况下（已排序）的时间复杂度为O(n)，最坏（倒序）为O(n^2)，平均情况下也是O(n^2)。它是一种稳定的排序算法，但效率较低。 2. 直接插入排序：将每个元素逐个插入到已排序的序列中的适当位置。在最好情况下（已排序）的时间复杂度为O(n)，最坏为O(n^2)，平均时间复杂度同样为O(n^2)。插入排序也是稳定的排序方法。 3. 选择排序：每次找到未排序部分的最大（或最小）元素，将其放在正确位置。无论输入顺序如何，选择排序的时间复杂度始终为O(n^2)，并且它是不稳定的排序算法。 4. 归并排序：采用分治策略，将大问题分解为小问题，然后合并这些小问题的解。归并排序在所有情况下都有O(n log n)的时间复杂度，是稳定的排序算法，适合处理大规模数据。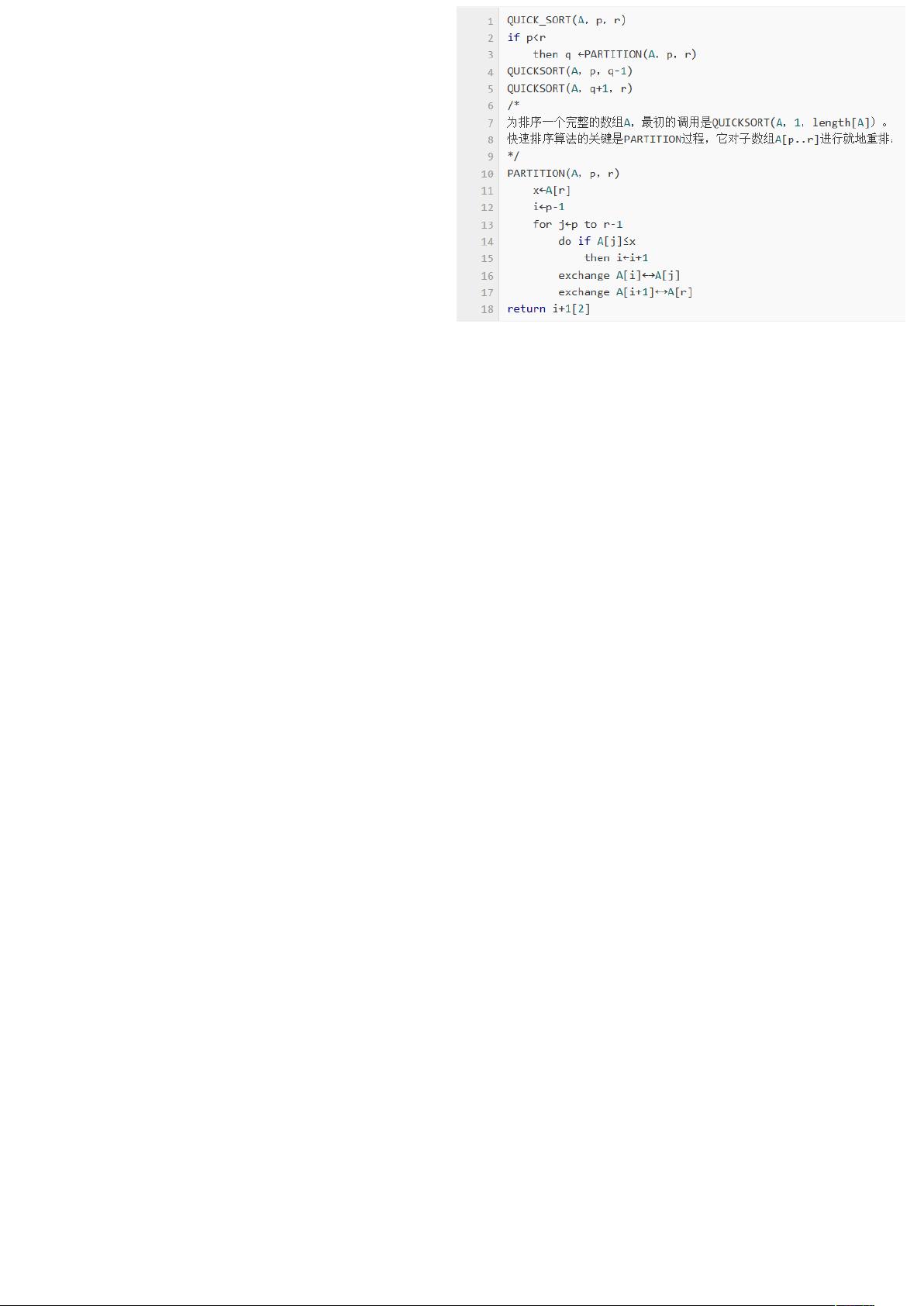 5. 快速排序：选择一个基准元素，将数组分为两部分，使得一部分的所有元素小于基准，另一部分的所有元素大于基准，然后对这两部分递归地进行快速排序。快速排序的平均时间复杂度为O(n log n)，最坏情况（已排序或逆序）为O(n^2)，但实际应用中通常表现优秀。 图上最短路径算法包括深度优先搜索(DFS)、广度优先搜索(BFS)、Dijkstra算法和Floyd算法，它们分别用于寻找单源最短路径和所有对最短路径。这些算法在路由、网络流量调度等领域有广泛应用。 最小生成树算法Kruskal和Prim是解决加权无向图的最小树问题，Kruskal算法基于边的集合选择，而Prim算法基于节点的集合选择，两者都能找到连接所有节点且总权重最小的树。 Hash，也称为哈希，是一种数据结构，它可以将任意大小的数据映射到固定大小的值，常用于快速查找和数据索引。 这些算法是IT初赛中常见的基础知识，理解和掌握它们对于编程和数据处理非常重要。深入学习这些概念，有助于提升解决问题的能力。