Gslib库与地质统计学：应用指南

需积分: 50 67 浏览量更新于2024-07-17 1 收藏 16.38MB PDF 举报

"GSLIB- Geostatistical Software Library and User Guide.pdf" 是一份由斯坦福大学的 Clayton V. Deutsch 和 Andre G. Journel 编写的关于地质统计学软件库的文档，旨在为用户提供地质统计分析的工具和指南。这本书是第二版，包含了 Andre G. Journel 的《Geostatistics for Natural Resources Evaluation》和 Edward H. Isaaks 及 R. Mohan Srivastava 的《An Introduction to Applied Geostatistics》等系列作品的一部分理念。 GSLIB (Geostatistical Software Library) 是一个用于地球科学、环境科学和工程领域的统计分析工具集，特别关注地质数据的建模和插值。这个库提供了一系列算法，包括但不限于： 1. 变差函数（Variogram）：变差函数是地质统计学中的核心概念，它描述了空间数据在不同距离上的变化程度。GSLIB 提供了计算和拟合变差函数的方法，帮助用户理解数据的空间结构并建立合适的模型。 2. Kriging 插值：Kriging 是一种基于变差函数的高级插值方法，能够估计未观测点的值，并给出估计误差的不确定性。GSLIB 包含了普通 Kriging、简单 Kriging、泛函 Kriging 等多种 Kriging 方法。 3. 密度估计：GSLIB 提供了估计数据分布密度的工具，这对于理解数据的集中趋势和分布特征至关重要。 4. 数据处理：包括数据清理、转换、标准化等预处理步骤，确保数据分析的准确性和有效性。 5. 图形和可视化：GSLIB 还包含了绘制各种地质统计图的功能，如变差函数图、半方差图、Kriging 预测结果图等，帮助用户直观地理解和解释数据。 6. 分区统计：对于大规模数据集，GSLIB 提供分区统计方法，可以将数据划分为多个区域并分别进行统计分析，简化复杂问题。 7. 聚类和分类：GSLIB 支持对地质特征进行聚类分析，有助于发现数据的内在模式和分类。通过 GSLIB，用户可以进行高级的地质统计分析，为资源评估、环境影响评估、矿产勘探等领域提供科学的决策支持。该软件库不仅适用于专业地质学家，也为其他领域的研究人员提供了强大的数据处理和分析工具。

CHAPTER

II. GETTING STARTED

xmn

East

axis)

...

Figure 11.1:

Plan

and vertical cross-section views that illustrate the

grid definition

used

GSLIB.

will be the number of lines in the file minus

nvari-2

minus the num-

ber of missing values. The programs read numerical values and

not

alphanumeric characters; alphanumeric varidbkes may be transformed

**.*

to integers or the source code modified.

xsiz

I+-

**..

b.0.

.*em

11.2.3

Grid Definition

Regular grids of data points or block values are often considered

input or

output. The conventions used throughout

GSLIB

are:

The

axis is associated to the east direction. Grid node indices

increase from

to nx in the positive

direction, i.e., to the east.

The

axis is associated to the north direction. Grid node indices iy

increase from

to ny in the positive y direction, i.e., to the north.

The

axis is associated to the elevation. Grid node indices iz increase

from

to nz in the positive

direction, i.e., upward.

The user can associate these three axes to any coordinates system that is

appropriate for the problem at hand. For example, if the phenomenon being

studied is

stratigraphic unit, then some type of stratigraphic coordinates

relative to

marker horizon could make the most sense

[48,

92, 1081. The

user must perform the coordinate transformation; there is no allowance for

rotation or stratigraphic grids within the existing set of subroutines.

The coordinate system is established by specifying the coordinates at the

center of the first block (xmn, ymn, zmn), the number of blockslgrid nodes

(nx, ny, nz), and the

size/spacing of the blocks/nodes (xsiz, ysiz, zsiz). Fig-

ure 11.1 illustrates these parameters on two 2D sectional views.

Sometimes

special ordering is used to store a ~egular grid. This avoids

+hr

rnr~~~i~mqont

~tgring

qcdn

rnorr\inptps

?rid

ipCl.ime

The

nrrlnr.mq

11.2.

GSLIB CONVENTIONS

point by point to the east, then row by row to the north, and finally level

level upward, i.e., x cycles fastest, then y, and finally

The index location

of any particular node is, iy, iz can be located by:

loc

(iz

nx *ny

(iy

122

Given the above one-dimensional index location of a node the three coordinate

indicels can be calculated

as:

oc-

int

(L)

lo;

(iz

int

loc

(iz

(iy

The uncompressed ASCII format is convenient because of its machine

independence and easy access by visual editors; however, a binary compressed

format would be most efficient and even necessary if large

grids are being

considered.

11.2.4

Program

Execution

and Parameter Files

The default driver programs read the name of

parameter file from standard

input

If the parameter file is named for the program and has a ".parn

extension, then simply keying a carriage return will be sufficient

(e.g., the

program

gam

would automatically look for

[mp.

All of the program

variables and names of input/output files are contained in the parameter file.

ty~~ical parameter file

illustrated in Figure 11.2. The pser can have

many lines of comments at the top of the file

desired, but formatted input is

started immediately after the characters "START" are found at the beginning

of a line. Some in-line documentation is available to supplement the detailed

documentation provided in this user's manual. Example parameter files are

included with the presentation of each program in Chapters

I11 through

and Appendix

An interactive and "error checking" user interface would help make GSLIB

programs more user friendly. A graphical user interface

(GUI)

has been

avoided because there is no single GUI that works on all computers. A use-

ful addition to each program would be an

intellzgent

interpretation program

that would read each parameter file and create a verbose English language

description

of the "job" being described by the parameters.

When a serious error is encountered, an error message is written to stan-

dard output and the program is stopped. Less serious problems or apparent

inconsistencies cause a warning to be written to standard output or a debug-

minq

(?I(>

qprl

tho

qrnrrrqir-

.\.rll

rnpt:-,,n

CHAPTER II. GETTING STARTED

Parameters

for

HISTPLT

***~*****.******.*****

START

PARAMETERS:

/data/cluster.dat

3 a

-1.

Oe21

histplt.ps

0.01

100.0

-1.

200

Clustered

Data

1.5

-1.1e21

\file

with

data

columns

for

variable

and

weight

trimming

limi

\file

for

PostScript

output

\attribute

minimum

and

maximum

\frequency

maximum

«0

for

automatic)

\number

classes

\O=arithmetic,

l=log

scaling

\O=frequency,

l=cumulative

histogram

\ number

cum.

qual1tiles

«0

for

all)

\number

decimal

places

«0

for

auto.)

\title

\positioning

stats

R',

-1

\reference

value

for

box

plot

Figure

11.2:

example

parameter

file

for

histplt.

1I.2.5

Machine

Precision

When calculations are performed on a computer, each arithmetic operation

generally affected by roundoff error. This error arises because the machine

hardware can only represent a subset of the real numbers

[69].

Roundoff error

not a major concern because the size of geostatistical matrices

typically

small. Large problems are often separated into a large number of smaller

problems by adopting local search neighborhoods.

Roundoff error

noticed most in the matrix solution of kriging systems;

storing the matrix entries in single precision causes the kriging weights ob-

tained from two different solution methods to change as soon as the third

decimal place. For this reason, all matrix inversion subroutines in GSLIB

have been coded in double precision. To save on storage, however, the

simulation program

luaim

(V.6.2)

coded in single precision. Roundoff error

becomes significant only when simulating very large grid systems.

Another source of imprecision

due

numerical approximations to cer-

tain.mathematical functions. For example, the cumulative normal distribu-

tion p

G(z) and inverse cumulative normal distribution y =

a-I

(p)

have

no closed-form expression and polynomial approxima.tions are used

[116J.

Im-

precision in these approximations

small relative to the error introduced by

. the floating-point representation of real numbers.

II.3

Variogram

Model

Specification

This section can be scanned quickly the first time through. The conventions

for describing a variogram model are explained here rather tha.n within all

kriging and simulation programs. Most of the kriging and simulation sub-

routines call for covariance or pseudo-covariance values; however,

a semivari-

ogram model rather than a covariance model must be specified. This apparent

II.

VARIOGRAM

MODEL

SPECIFICATION

inconsistency allows

for

the traditional practice of modeling variograms and

also permits the straightforward incorporation of the power model, which has

no covariance counterpart.

An acceptable semivariogram model

for

GSLIB consists of an isotropic

nugget effect

and any positive linear combination of the following standard

semivariogram models:

Spherical

model defined

an actual range a and positive variance

contribution or

sill value

(11.15)

Exponential

model defined

an effective range

a (integral range

a/3) and positive variance contribution value

(II.16)

Gaussian

model defined by an effective range a and positive variance

contribution value

(11.17)

Power

model

defined

a power 0 < w < 2 and positive slope

(ILl8)

The distance h may be anisotropic in

or 3D.

Hole

effect

model defined

a length a to the first peak (size of the

underlying cyclic features) and positive variance contribution value

'."'

f(h)

c·

[1.0 - cos

11')

]

(lI.19)

be a legitimate positive definite variogram model, this hole effect

model may only be applied in one direction;

that

is, the variogram

4Anisotropic nugget effects can be modeled

setting some of the directional ranges of

the

firnt nested

structure

to a very small value.

5For variogram models

that

reach their sills c asymptotically, the effective range

defined as the distance

which

.,.(a)

0.95·

6Note

that

matrix

instability problems are often encountered with a Gaussian model

with

nugget effect [153, 173J. Also, a Gaussian variogram model with no nugget effect

should not be used

for

categorical variables

[137].

7The power model is associated to self-affine random fractals with the parameter w

relatE!d

the fractal dimension D by the relation: D = E + 1 - w/2, where E

the

topological dimension of the space

(E=l,

[80,

184).

CHAPTER

11.

GETTING STARTED

axis

Major Direction of Continuity

(North)

Rotated

axls

(N30E)

degrees

angle

ang

maximum range

a-hrnax

minimum range

a-hmin

Figure

IL3:

example

the

two parameters needed to

define

the geometric

anisotropy of a variograrn structure

2D.

specified by the direction of the hole effect, the range parameter in that

direction, and very large range parameters in the two other directions,

say, 1.0e21.

Although not allowed for in the parameter files, a dampened hole effect

model is

also coded in the cova3 subroutine. The dampened hole effect

model is:

where

is the distance at which

95%

of the hole effect is dampened out

(the variance magnitude of the periodic component is then

c).

'The type of variogram structure is specified by an integer code, which

is the order in the above list, i.e., it=l: spherical model, it=2: exponential

model,

it=3:

Gaussian model,

it=4:

power model, and it=5: hole effect

model. The

and

parameter values, which correspond to the description

in the above list, are also needed.

Each nested structure requires an

additional two or five parameters that

define its own geometric anisotropy in

3D.

Figure

11.3

illustrates the

angle and range parameters required in 2D.

The direction of maximum continuity is specified by a rotation angle

ang

corresponding to an azimuth angle measured in degrees clockwise from the

positive

or north direction. The range in this horizontal naazimum direc-

tion is specified by

ahmaz.

The range in the perpendicular direction or the

horizontal minimum direction is specified by

ah,,,.

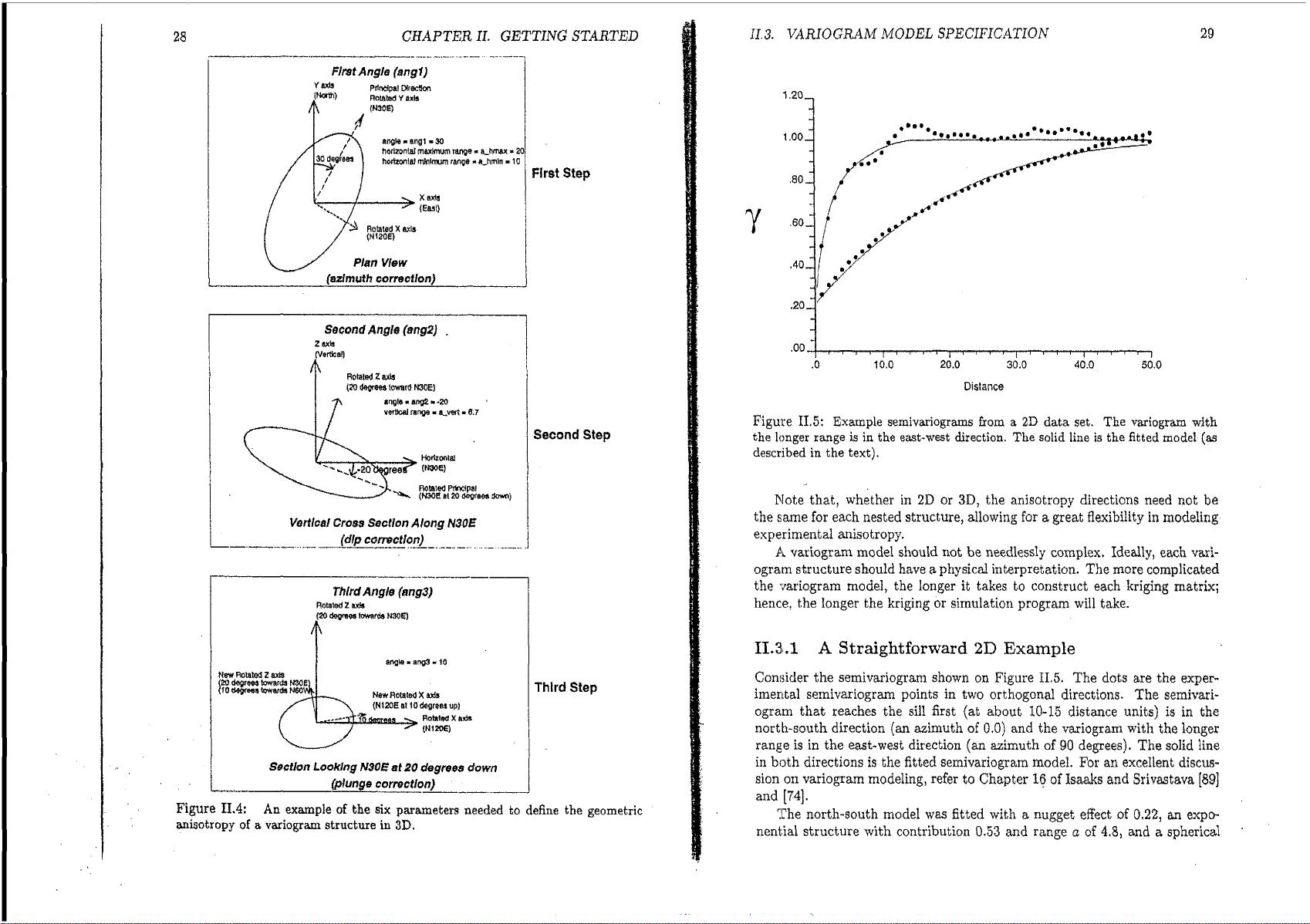
IL3.

VARIOGRAM

MODEL

SPECIFICATION

very large range implies that no variance contribution will

added to

that direction, a feature known

"zonal anisotropy."

Within the soRware the actual distance is corrected so that it accounts for

the specified anisotropy. That is, the distance component along the rotated

axis (see Figure

11.3)

is corrected by the ratio

ah,,,/ah,,,.

This convention

allows the anisotropy of the power model to be handled in an intuitively

correct manner; an anisotropic distance is calculated and the power

is left

unchmged.

Figure

11.4

illustrates the angles and ranges required in

3D.

Many software

packages take a shortcut and only use two angles and two ranges. The added

complexity of three angles is not in programming but in documentation. It is

quite straightlorward to visualize and document a phenomenon that is dipping

with respect to the horizontal at a dip azimuth that is not aligned with a

coordinate axis. The third angle is required to account for the geological

concept of a plunge or rake. One example that requires a third

angle

modeling the geometric anisotropy within the limbs uf a plunging syncline.

The easiest way to describe the three angles and three ranges is to imagine

the rotations and squeezing that would be required to transform

sphere

into an ellipsoid; see [65]. We will refer to the original

axis

the principal

direction and consider the rotations such that it ends

being the actual

principal structural direction (direction of maximum continuity):

The first rotation angle

angl

rotates the original

axis (principal

direction) in the horizontal plane: This angle is memured in degrees

clockwise.

The second rotation angle

ang2

rotates the principal direction from

the horizontal: This angle is measured in negative degrees down from

horizontal.

The third rotation angle

ang3

leaves the principal direction, defined

angl

and

ang2,

unchanged. The two directions orthogonal to that

principal direction are rotated clockwise relative to the principal direc-

tion when looking toward the origin. Thc rotation of the third step in

Figure

11.4

appears

counterclockwise since the view is away from the

origin.

Zonal anisotropy

can

be considered

a particular case of a geometric

anisotropy, see

[74]

and [89], pp. 385-386. This can be handled by entering the

appropriate range

a very large number; that particular variogram structure

is then added only to the orthogonal directions (say, across bedding). For

simulation purposes, a strong zonal anisotropy is better reproduced when the

simulation grid is aligned with the direction of zonal anisotropy.

The program

vmodel (see Section VI.2.8) will write out the model semi-

variogram in any number of arbitrary directions and lags. This will help

validate the correct entry of a semivariogram model.

CHAPTER

II.

GETTING STARTED

,,----------_.,---------,-,.-._.

First

Angle

(ang1)

P~noIp.1

OIreclion

RotaledVbls

(N30E)

angle.

angl

.30

horizontal

maximum

range.

s-h/1'l8Jl:

•

hori%onlaJ

mtnlcrom

range

"-.hmln

•

~--f.---=,..

axis

(EMI)

RotalodX

""Is

(NI20E)

Plan

View

(azimuth correction)

Second

Angle

(sng2)

Zbls

(Vertical)

Rotated

axis

(2Q

<lagre"

toward

N30E)

angle.

ang2

....

vertical

ral"108

-I.-vert. 6.7

Rotaled

Principal

(N30E

al2Q

dOll<aes

00wn)

Vertical

Cross

Sect/on

Along

H30E

__________

(dIp

cO!:..'!~!!()!'l_

...

__.

___

,......------------_._-_._-----

Third

Angle

(ang3)

AotaledZ

IlJ(I$

(2Q

1""",,<Is

N30E)

aog'" • ang3 •

New

Rotaled

axis

(NI2QE

all0

dejjre

up)

'-'==J.,I..I.II.lIIIWlis.....:,..

Rolllied X

axis

(NI2QE)

S9ct/on

Looking

H3DE st 20

degrees

down

(plunge

correctlo~

___

First

Step

Second

Step

Third

Step

Figure II.4:

example

the

six

parameters needed to

define

the geometric

anisotropy

variogram structure

3D.

IJ.3.

VARIOGRAM MODEL SPECIFICATION

1.20

1.00

.80

.60

.40

.20

•••••

•••••••••

•

•••••••

•..•••

···I.···:~

...

....

....-f'

....

d.~

/~.

.0 10.0

20.0

30.0 40.0

50.0

Distance

Figme

11.5:

Example semivariograms

from

data set. The

variogram

with

the

longer

range

the east-west direction. The solid

line

the fitted

model

(as

described

the text).

Note

that,

whether

3D,

the anisotropy directions need not be

the same for each nested structure, allowing for a great flexibility

modeling

experimental anisotropy.

PI.

variogram model should not be needlessly complex. Ideally, each vari-

ogram structure should have a physical interpretation. The more complicated

the variogram model, the longer it takes to construct each kriging matrix;

hence, the longer the kriging or simulation program

will

take.

11.3,.1

Straightforward

Example

Conilider

the

semivariogram shown on Figure II.S. The dots are the exper-

imental semivariogram points in two orthogonal directions. The semivari-

ogram

that

reaches the sill first

(at

about 10-15 distance units)

in the

north-south direction (an azimuth

0.0) and the variogram with the longer

range is in the east-west direction (an azimuth of

degrees). The solid line

both

directions

the fitted semivariogram model. For an excellent discus-

sion on variogram modeling, refer

Chapter

of Isaaks and Srivastava

[89]

and

[74J.

The

north-south model

was

fitted with a nugget effect of

0.22,

an expo-

nential

structure

with contribution 0.53 and range a

4.8, and a spherical

CHAPTER II. GETTING STARTED

structure with contribution

0.25

and

range 15.0.

The

east-west model was

fitted with nugget effect of

0.22,

exponential structure with contribution

0.53 and range a of

48.0,

and a spherical structure with contribution 0.25

and range

50.0.

The

semivariogram parameters required

the kriging or

simulation programs would be specified as follows:

::::

nugget::::

0.22

nst

number of nested structures:::: 2

(1)

:::::

type of first structure

2 (exponential)

azimuth

(1)

degrees (the east-west direction)

(1)

= contribution of first

structure

0.53

aahma:.:

(1)

= maximum range of first

structure

48.0

aahmin

(1)

= minimum range of first structure =

4.8

(2)

::::

type of·second structure = 1 (spherical).

azimuth

(2)

degrees (the east-west direction).

(2)

contribution of second structure:::: 0.25.

aahma.x

(2)

:::

maximum range

second structure

::=

50.0

aahmin

(2)

::=

minimum range of second structure

=:::

15.0

II.3.2

Example

with

Zonal

Anisotropy

Consider the semivariogram shown on Figure II.6.

The

dots are

the

experi-

mental semivariogram points in two orthogonal and principal directions.

The

semivariogram

that

reaches

the

higher sill

a direction

N60E

(an azimuth

60.0)

and

the semivariogram with the lower

sill

the perpendicular

direction (an azimuth of

150

degrees).

The

solid line in both directions

the

fitted semivariogram model.

The

semivariogram in the direction of maximum continuity (azimuth 150)

was modeled with a nugget effect of 0.40, a spherical structure with a contri-

bution of

DAD

and range of 300.0,

exponential structure with contribution

0.95

and

range of 4500.0, and a spherical structure with contribution 0.90 and

range

80000.0. Thus, for all practical purposes this last spherical structure

does

not

contribute

direction N150E.

The

sernivariogram with the higher

sill was fitted with a nugget effect of

0040,

a spherical structure with a contri·

bution of 0.40 and range of 100.0,

exponential structure with contribution

0.95 and range of 1500.0,

and

a spherical structure with contribution 0.90

and

range 1600,0. This semivariogram model would be specified

follows:

.r' _ ............

".-

\(1

II.

VARIOGRAM

MODEL

SPECIFICATION

3.00

2.50

2.00

.......

1>0 V

1.00 Y

.50

..........

.........

. .

...............

....

.00

-rr-r-r-r-r-rr-rrrr'.,...,..rr,-,-.,..,...,.-,-,.,....,...,...,...,..,....,....,.......~~-

1000. 2000. 3000. 4000. 5000. 6000. 7000.

Distance

F.igure

~I.~:

Example semivariograms

from

data set.

The

variogram with the

lllghe.r

stll.ls at azimuth

degrees

(N60E).

The

Bolid

line

the fitted

model

(as

descnbed

III

the text).

剩余188页未读，继续阅读

CSRF-CN

粉丝: 0
资源: 1

Gslib库与地质统计学：应用指南

GSLIB2.6(ARMSDT)

GSLIB_Geostatistic_地质统计学工具书_gslib_

地质统计程序库Gslib介绍资料

【GSLIB核心概念入门】：成为Geostatistical Software Library专家的5个秘密步骤

IMG2GSLIB:将图像转换为GSLIB网格-NEW：3D支持。-开源

MATLAB克里格工具箱中文翻译版.pdf

(完整word版)地统计学总结.pdf

gslib_src_0.8.zip

sgems.tar.gz_gslib_sgems_地质统计学

GsLIB for GAMEBOYAdvance

最新资源