MATLAB实现经典隶属函数：高斯、双边高斯与一般钟型

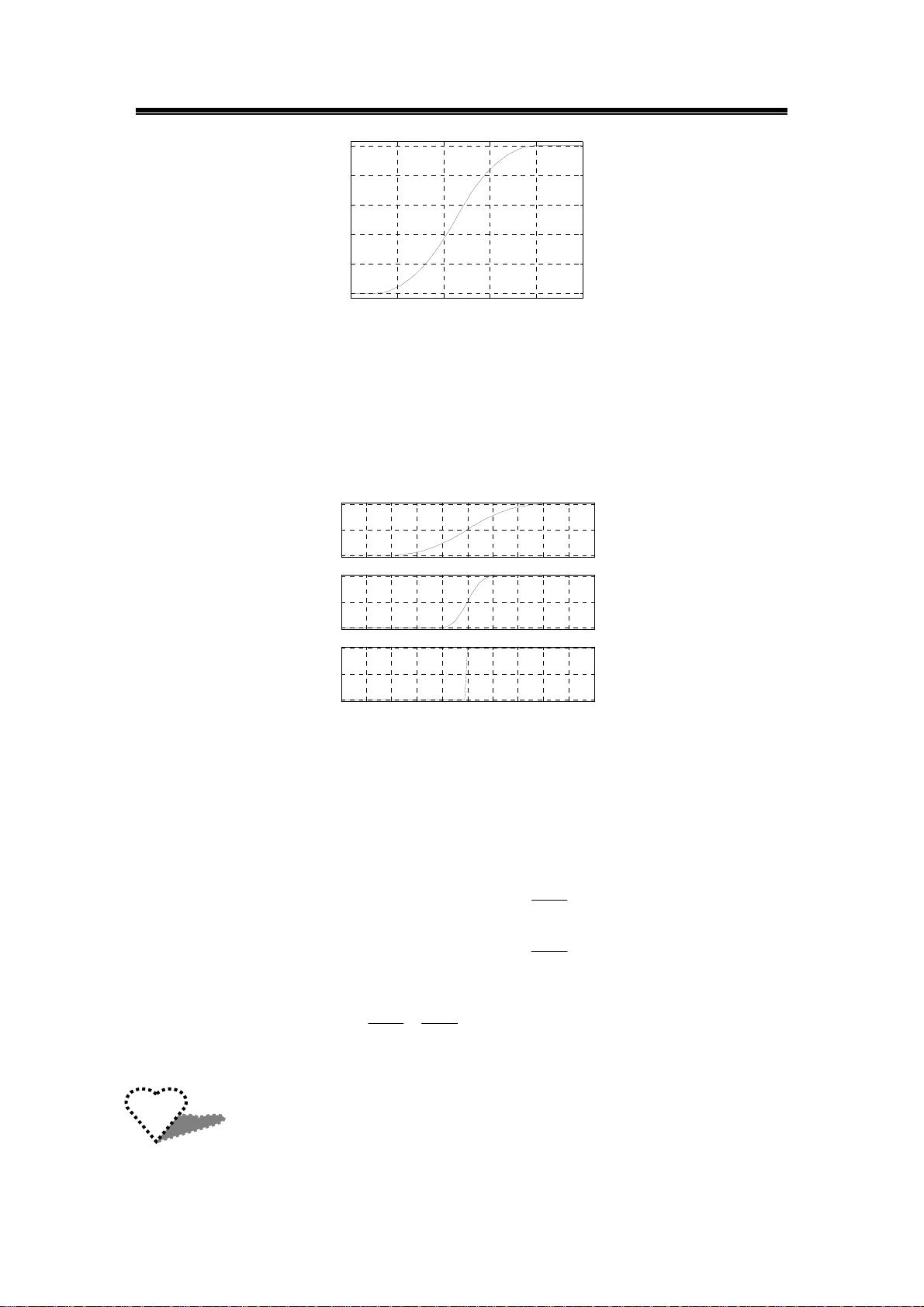
本章节详细介绍了如何在MATLAB中使用隶属函数进行模糊逻辑建模。隶属函数是模糊系统的基础，它们将不确定性和模糊性转化为可处理的数据形式。这里主要讲解了三种常见的隶属函数类型：高斯隶属函数、两边型高斯隶属函数以及一般钟型隶属函数。 1. 高斯隶属函数 (gaussmf): 这是一种常用的模糊集表示方法，其数学表达式为 \( \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{(x-c)^2}{2\sigma^2}} \)，其中 \( c \) 和 \( \sigma \) 是参数，分别代表中心位置和标准偏差。通过`gaussmf`函数实现，如例6-1所示，通过改变参数可以调整函数的形状和宽度，生成的图形直观展示了函数特性。 2. 两边型高斯隶属函数 (gauss2mf): 这种函数结合了两个独立的高斯函数，参数包括两个中心位置 \( c_1 \) 和 \( c_2 \)，以及对应的宽度 \( \sigma_1 \) 和 \( \sigma_2 \)。例子6-2展示了如何通过改变这些参数来绘制不同形状的函数图形。 3. 一般钟型隶属函数 (gbellmf): 也称为bellmf函数，它不像高斯函数那样对称，具有更尖锐的峰值。这种函数的数学表达式依赖于三个参数 \( a \), \( b \), 和 \( c \)，其中 \( b \) 控制峰值的陡峭程度，\( c \) 定义峰值位置。例6-3展示了如何使用`gbellmf`函数创建此类函数及其图形。 这些函数在MATLAB中提供了灵活的方法来构建模糊系统的输入输出映射，帮助设计者处理不确定性的决策问题。通过这些函数，用户能够可视化不同的隶属度变化，并根据实际应用场景调整函数的形式，从而实现模糊逻辑的精确控制和分析。理解并熟练运用这些工具对于模糊控制系统的设计和优化至关重要。