递归与分治算法详解：从阶乘到 Ackerman 函数

"这篇资料主要介绍了递归和分治这两种重要的算法设计策略，通过实例解析了递归的基本概念，包括阶乘函数、Fibonacci数列以及 Ackerman 函数，并探讨了递归函数的边界条件和递归方程。同时，提到了分治算法的应用，虽然具体内容未涉及，但可以推测资料可能还涵盖了如何将问题分解为子问题并合并解决方案的分治方法。" **递归算法** 递归是一种强大的编程技巧，它允许函数通过调用自身来解决问题。递归算法的核心有两个关键组成部分：边界条件和递归方程。边界条件是递归终止的依据，确保算法最终能够停止；而递归方程则描述了如何将问题分解成更小的部分。例如，阶乘函数 `n!` 的边界条件是 `n=0` 时 `n! = 1`，递归方程是 `n! = n * (n-1)!`。 **实例分析** 1. **阶乘函数**：`n!` 可以通过递归定义为 `n! = n * (n-1)!`，其中 `n=0` 是边界条件，使得 `0! = 1`。这种递归定义使得算法简洁易懂。 2. **Fibonacci数列**：Fibonacci数列是递归定义的另一个经典例子。数列的每个元素可以通过前两个元素相加得到，即 `F(n) = F(n-1) + F(n-2)`，边界条件是 `F(0) = 1` 和 `F(1) = 1`。 3. **Ackerman函数**： Ackerman 函数展示了双递归的概念，其中变量 `m` 的不同值导致单变量函数。这个函数的特殊之处在于，它无法找到一个非递归的定义。随着 `m` 的增加，函数的增长速度极快，甚至超出数学表达式的范围。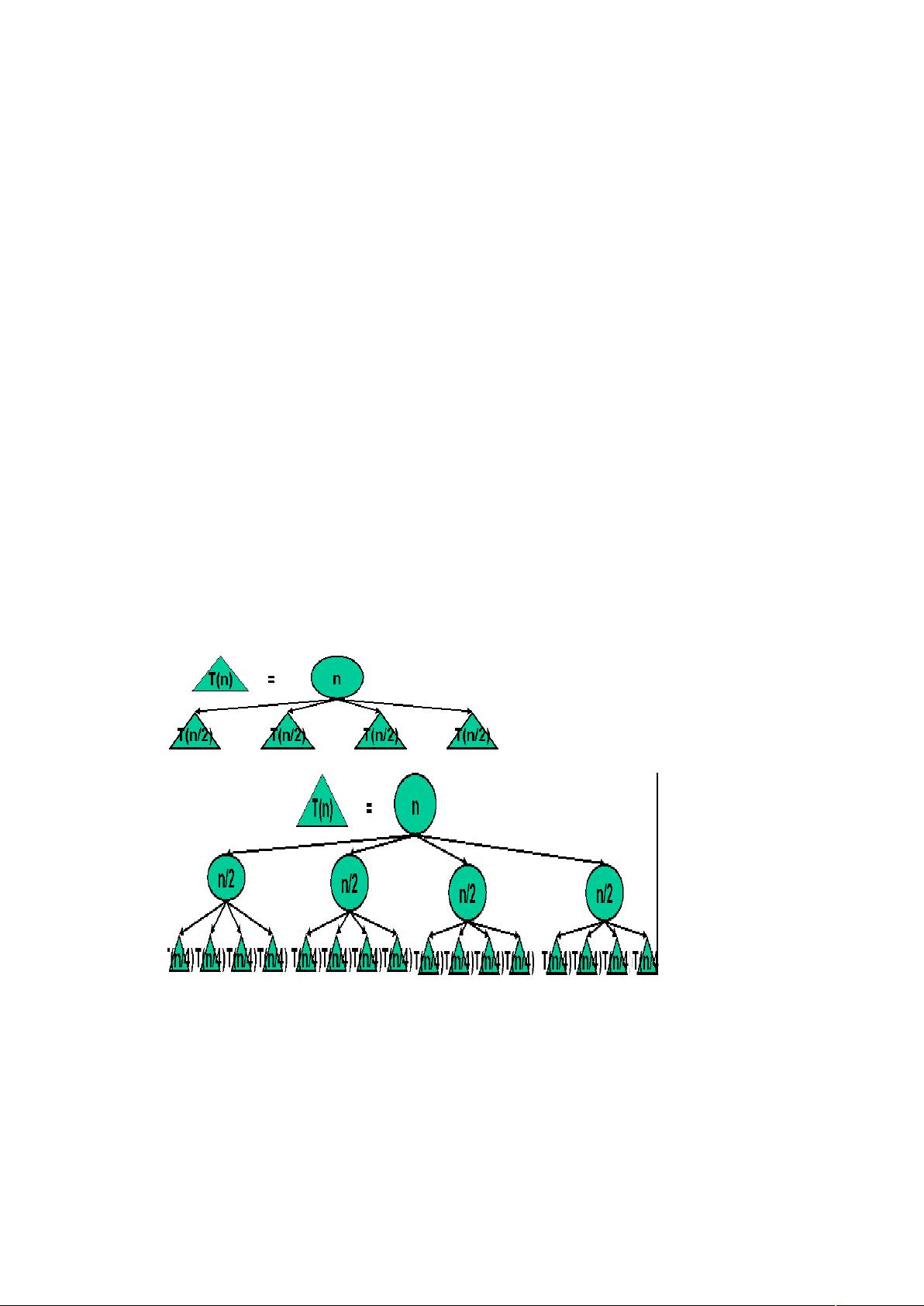 **分治算法** 分治策略是一种将大问题分解为多个小问题进行解决的方法。基本步骤包括： 1. **分解**：将原始问题拆分为多个规模较小的相同或相似子问题。 2. **解决**：递归地解决这些子问题。 3. **合并**：将子问题的解组合起来，得到原始问题的解。 虽然本文没有深入讨论分治算法的具体实现，但可以举例说明，如快速排序、归并排序和Master定理都是分治算法的经典应用。在这些算法中，问题被不断分割，直到达到可以直接解决的小规模问题，然后将结果整合以解决原问题。 **复杂度分析** 在算法分析中，递归函数如Ackerman函数和它的拟逆函数α(n)常常被用来探讨复杂度。尽管对于实际的正整数n，α(n)通常不会太大，但在理论层面上，α(n)的增长没有上界，这强调了递归函数可能带来的计算复杂性。 递归和分治是算法设计的重要工具，它们能帮助我们解决各种复杂问题。理解递归的边界条件和递归方程，以及掌握如何将问题分解为子问题，是提升编程能力和算法设计能力的关键。在实际应用中，应谨慎使用递归，因为不当的递归可能导致效率低下或栈溢出等问题。同时，合理利用分治策略可以优化算法的效率和可读性。