小波变换基础与Haar小波详解

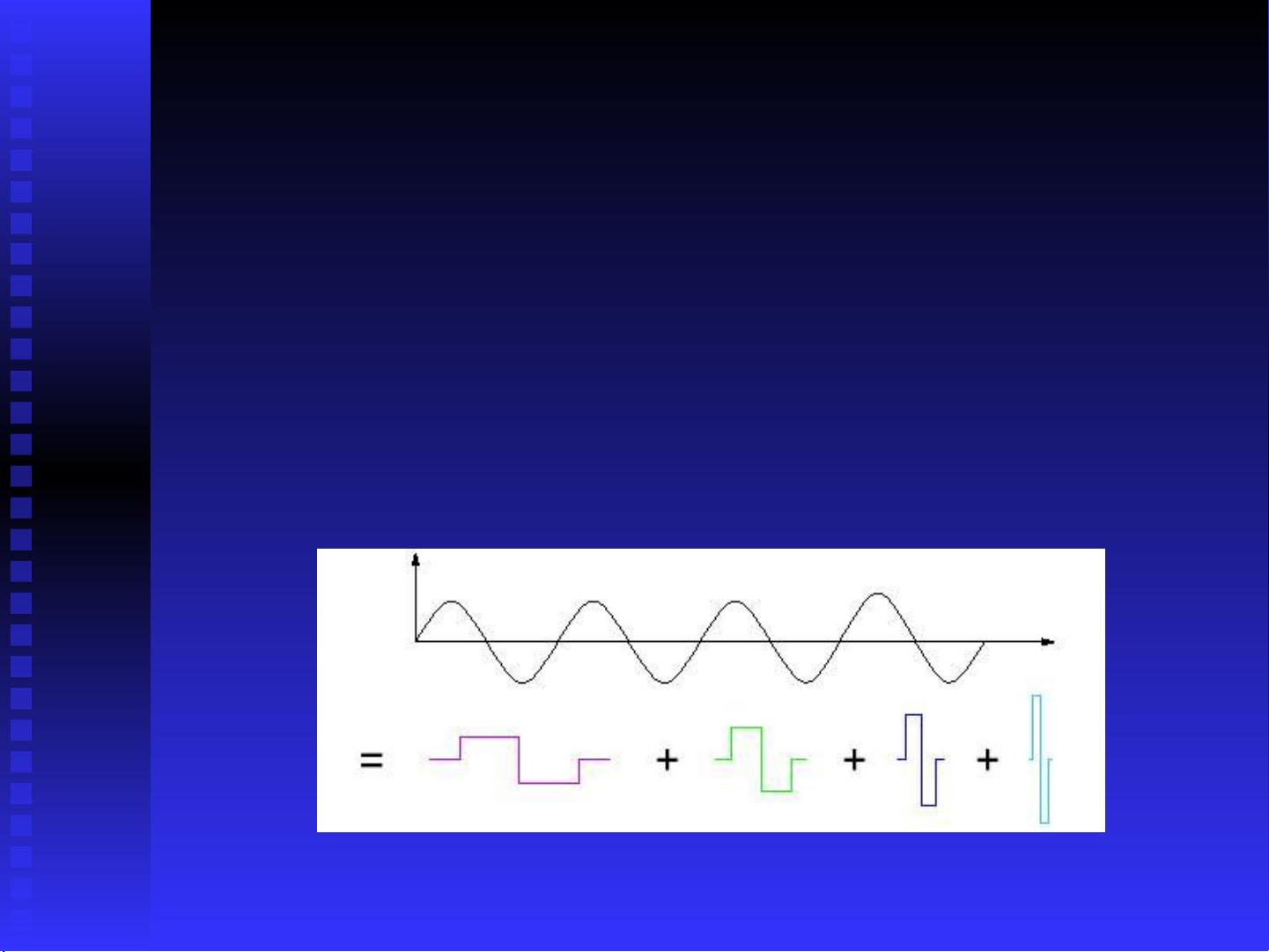
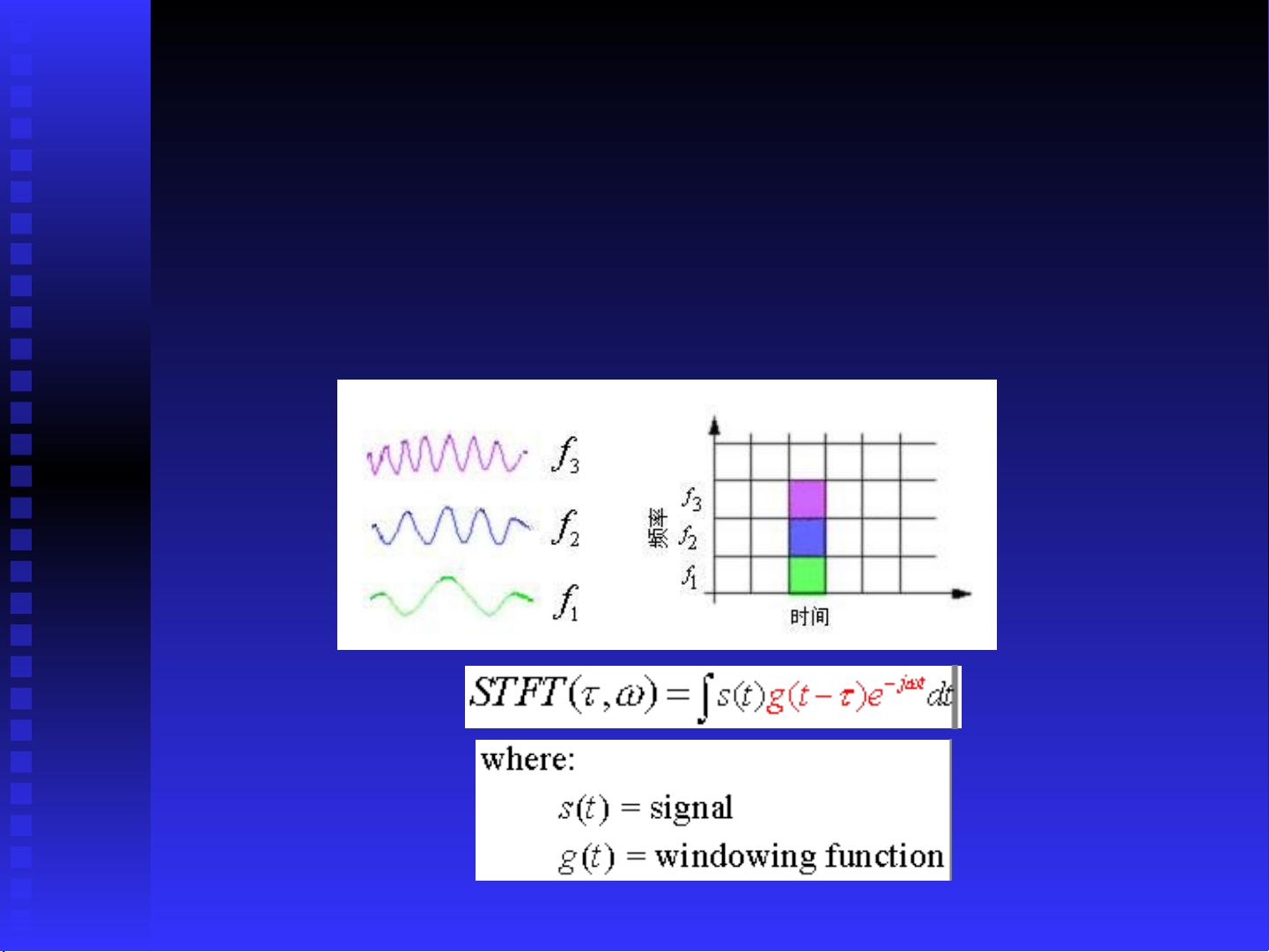
"小波变换的原理及编码" 小波变换是一种在信号处理和图像分析等领域广泛应用的数学方法，它是傅立叶分析后的重大进展。小波变换的主要特点是能够同时在时间和频率上对信号进行局部分析，这使得它在处理非平稳信号时尤其有效。 一、小波变换 1. 小波：小波是一种具有有限持续时间的函数，其频率和振幅会发生突然变化。与正弦波不同，小波通常是非规则且不对称的，其在整个时间范围内的平均幅度为零。这些特性使小波能够更好地捕捉信号的局部特征。 2. 小波变换：通过小波函数与原始信号的卷积或乘积，可以得到不同尺度和位置的小波系数，这些系数反映了信号在不同时间和频率上的分布情况。 3. 离散小波变换（DWT）：离散小波变换是小波变换的实用形式，通常用于实际的数字信号处理。DWT将信号分解为一系列低频和高频成分，便于分析和压缩。 二、Haar小波变换 1. 哈尔函数：Haar小波是最简单的小波类型，由简单的阶跃函数构成，常用于教学和简单应用中。 2. 求均值和差值：Haar小波变换通过计算信号的相邻部分的平均值和差值来进行。 3. 哈尔变换的特性：Haar小波变换具有计算简单和对称性的特点，但其表达能力相对有限。 4. 一维哈尔小波变换：在一维信号处理中，Haar小波用于分解信号，提取不同尺度的信息。 5. 二维哈尔小波变换：在图像处理中，二维Haar小波变换可以分析图像的局部特征。 三、小波变换的应用 小波变换广泛应用于图像压缩、信号去噪、故障诊断、模式识别、数据压缩等多个领域。例如，在图像处理中，小波变换可以有效地分离图像的不同细节层次，从而实现高效的压缩和重建；在语音分析中，小波变换可以揭示语音信号的时间-频率结构，有助于语音识别和增强。 小波变换提供了一种强大的工具，能够对复杂信号进行多分辨率分析，对于初学者来说，理解小波的基本概念、特性和应用是十分重要的。通过学习小波变换，不仅可以掌握一种重要的数学工具，还能为深入研究相关领域的高级技术打下坚实的基础。