维特比算法：动态规划解决隐马尔可夫模型

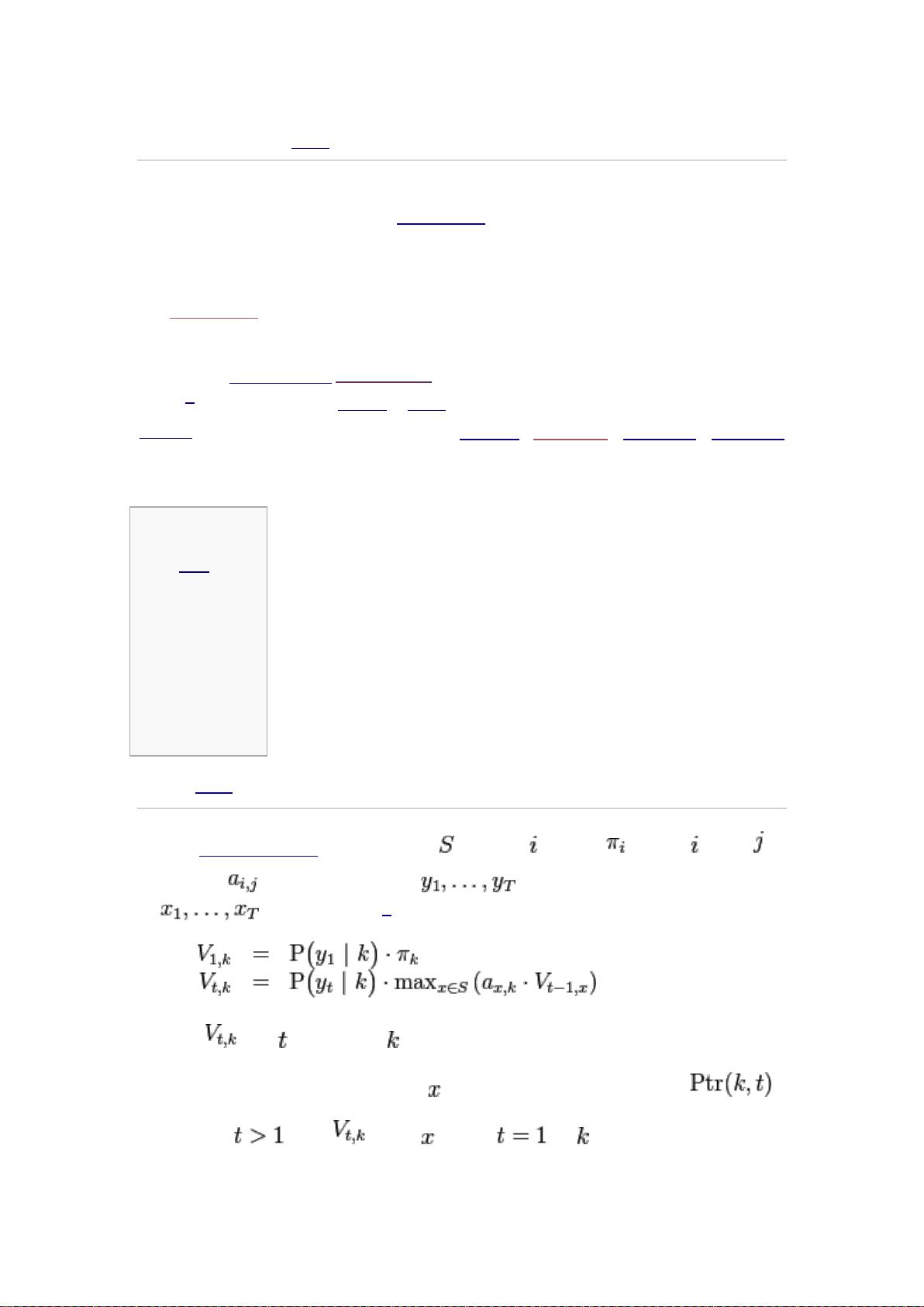
"维特比算法是用于解决最优化问题的一种动态规划算法，由安德鲁·维特比在1967年提出，最初应用于数字通信中的解卷积问题，现在广泛应用于语音识别、关键词识别、生物信息学等多个领域。它在隐马尔可夫模型(HMM)中寻找最可能的隐藏状态序列，即‘维特比路径’，以解释给定的观测事件序列。" 维特比算法的核心在于通过递推关系找到最优路径。对于一个给定的隐马尔可夫模型，其状态空间为S，初始状态概率为π，状态转移概率为A（A[i][j]表示从状态i转移到状态j的概率），以及观测输出序列O。算法的目标是找到最有可能产生这个观测序列的隐藏状态序列。 算法步骤如下： 1. 初始化：计算在观察序列的第一个时刻，所有状态作为起始状态的概率。记为V[0][s] = π[s] * P(O[0]|s)，其中P(O[0]|s)是状态s产生第一个观测O[0]的概率。 2. 递推：对于每个时间步t (1≤ t ≤ T)，遍历所有状态s'，计算从状态s到状态s'再到状态s''的概率，并与之前时刻的最优概率相乘，即V[t][s'] = max(V[t-1][s] * A[s][s']) * P(O[t]|s')，其中s是状态s'在时刻t-1的前驱状态。 3. 向后指针：记录下每个状态s'在时刻t的最佳前驱状态，这可以通过保存V[t][s']最大值对应的s来实现。 4. 回溯：从最后一个时间步开始，通过向后指针回溯，可以构建出最有可能的隐藏状态序列。 5. 结果：最终的维特比路径就是通过回溯得到的状态序列，而该路径的总概率就是V[T][s]，其中s是T时刻最优状态。 伪代码如下： ``` for t = 1 to T: for s in S: V[t][s] = 0 BP[t][s] = None for s in S: for s' in S: prob = V[t-1][s'] * A[s'][s] * E[s][O[t]] if prob > V[t][s]: V[t][s] = prob BP[t][s] = s' BP[T] contains the final state of the Viterbi path Backtrack from BP[T] using BP array to construct the optimal state sequence ``` 例子：在语音识别中，声学特征序列O被视为观测，单词序列W视为隐藏状态。通过维特比算法，我们可以找到最有可能的单词序列，使得它产生的声学特征与实际观测最为匹配。 注：维特比算法的复杂度为O(T*|S|^2)，其中T是观测序列的长度，|S|是状态空间的大小。虽然在大规模问题中可能会面临效率问题，但其在很多情况下仍然是解决问题的有效工具，尤其在存在局部最优解的情况下。 参考资料：维特比算法的详细介绍可以在各种信息理论、信号处理、机器学习和自然语言处理的教材中找到，如《统计语音识别》、《隐马尔可夫模型及其应用》等。