自编MATLAB FFT程序实现数字信号处理

该资源是一个MATLAB代码，用于实现自编的快速傅立叶变换（FFT）程序。程序包括两个函数：`mydft` 和 `myfft`，前者用于计算离散傅立叶变换（DFT），后者是基于基2的FFT算法。此代码适用于数字信号处理的上机实验，旨在帮助用户理解和掌握DFT和FFT的基本概念及MATLAB编程技巧。 在数字信号处理领域，傅立叶变换是一种重要的分析工具，它能够将时域信号转换到频域，以便分析信号的频率成分。离散傅立叶变换（DFT）是连续傅立叶变换在离散时间域中的近似，适用于处理离散信号。DFT的计算量较大，尤其是对于大数据量的序列，计算复杂度是O(N^2)。 快速傅立叶变换（FFT）是一种高效的计算DFT的方法，其运行时间复杂度为O(N log N)，显著降低了计算成本。该代码中的`myfft`函数采用的是基2的FFT算法，即Cooley-Tukey算法，通过递归地将序列分为两半，然后进行蝶形运算，大大减少了计算量。 在`myfft`函数中，首先检查输入序列的长度，如果长度为1，直接返回序列本身，因为长度为1的序列其FFT就是自身。否则，找到最接近序列长度的2的幂次，然后将序列拆分为偶数和奇数部分，分别对这两部分进行FFT，再通过蝶形运算组合结果。蝶形运算涉及到复数指数项WN，这个项随着迭代逐步减小序列的旋转因子。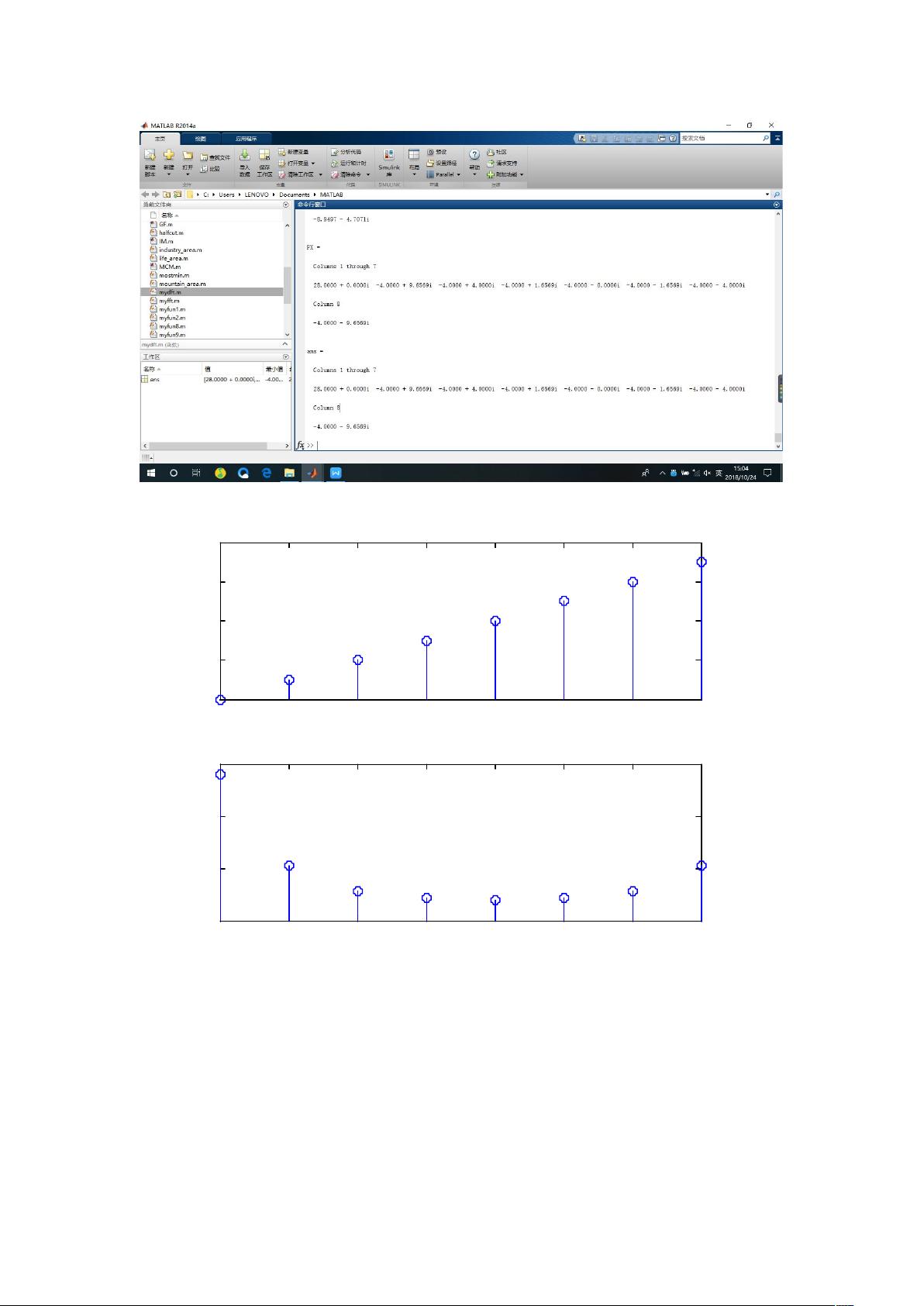 实验目的是使学习者理解DFT和FFT的概念，熟悉MATLAB编程，并通过可视化输出观察信号的时域和频域表示。代码中的`subplot`函数用于创建多子图，展示原始信号x(n)以及其对应的频谱|FX(k)|，帮助直观地理解变换过程。 这段代码是数字信号处理教学中的一个重要实践，它提供了实现DFT和FFT的基础，并结合MATLAB图形界面，便于用户学习和验证理论知识。通过运行此代码，学习者可以深入理解离散傅立叶变换及其快速算法在实际应用中的作用和效果。