使用抛物线法解决最优化问题的C++实现

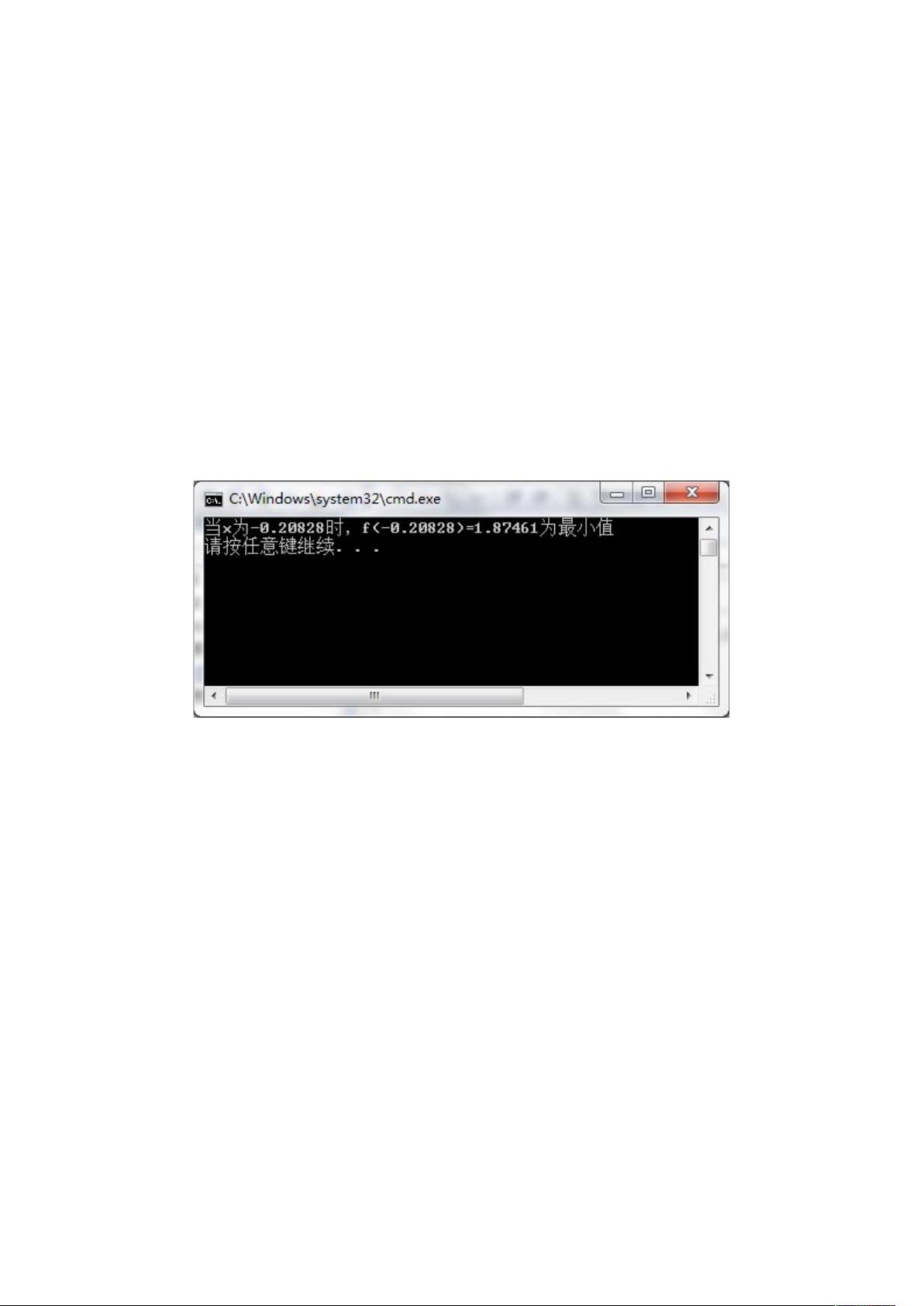
"这篇内容是关于大连理工大学的一份最优化方法作业，主要涉及了两种优化算法的实现：抛物线法和成功失败法。代码分别用C++编写，用于求解一元多项式的局部最小值。" 在最优化方法中，目标是找到一个函数的最优解，通常是全局最小值或最大值。这篇作业提供了两个不同的搜索策略来逼近这个最优解。第一部分介绍的是抛物线法，这是一种基于三点插值的迭代方法，适用于寻找一维函数的局部最小值。 抛物线法的工作原理如下： 1. 给定三个点t0、t1和t2，首先计算通过这三个点的抛物线方程。 2. 然后找到这个抛物线的顶点xt，即可能的极小值点。 3. 判断xt是否满足收敛条件，即xt与t0之间的差的绝对值小于预设的阈值eclipse（这里设置为0.001）且f(xt)比f(t0)更小。 4. 如果满足条件，则xt就是局部最小值；如果不满足，根据xt与t0、t1、t2的关系更新这三个点的位置，继续迭代。 第二部分提到的是成功失败法，也称为黄金分割法或者二分搜索的一种变体，它通常用于在一维区间内寻找函数的极值。不过，这部分的代码不完整，只给出了函数名和包含头文件的部分。 在实际应用中，最优化方法广泛应用于工程问题、数据分析、机器学习模型的参数调优等。抛物线法和成功失败法都是数值优化中的基础算法，虽然它们简单，但在特定条件下效率较高，易于理解和实现。 这份作业旨在帮助学生掌握最优化的基本思想和方法，并通过编程实践来提升对这些概念的理解。通过对这两种方法的实现，学生可以了解到如何逐步逼近函数的最小值，并理解在实际问题中如何选择和应用优化算法。