3
0 50 100 150
0
0.01
0.02
0.03
0.04
0.05
0.06
0.07
number of points used to estimate pose
computation time (sec)
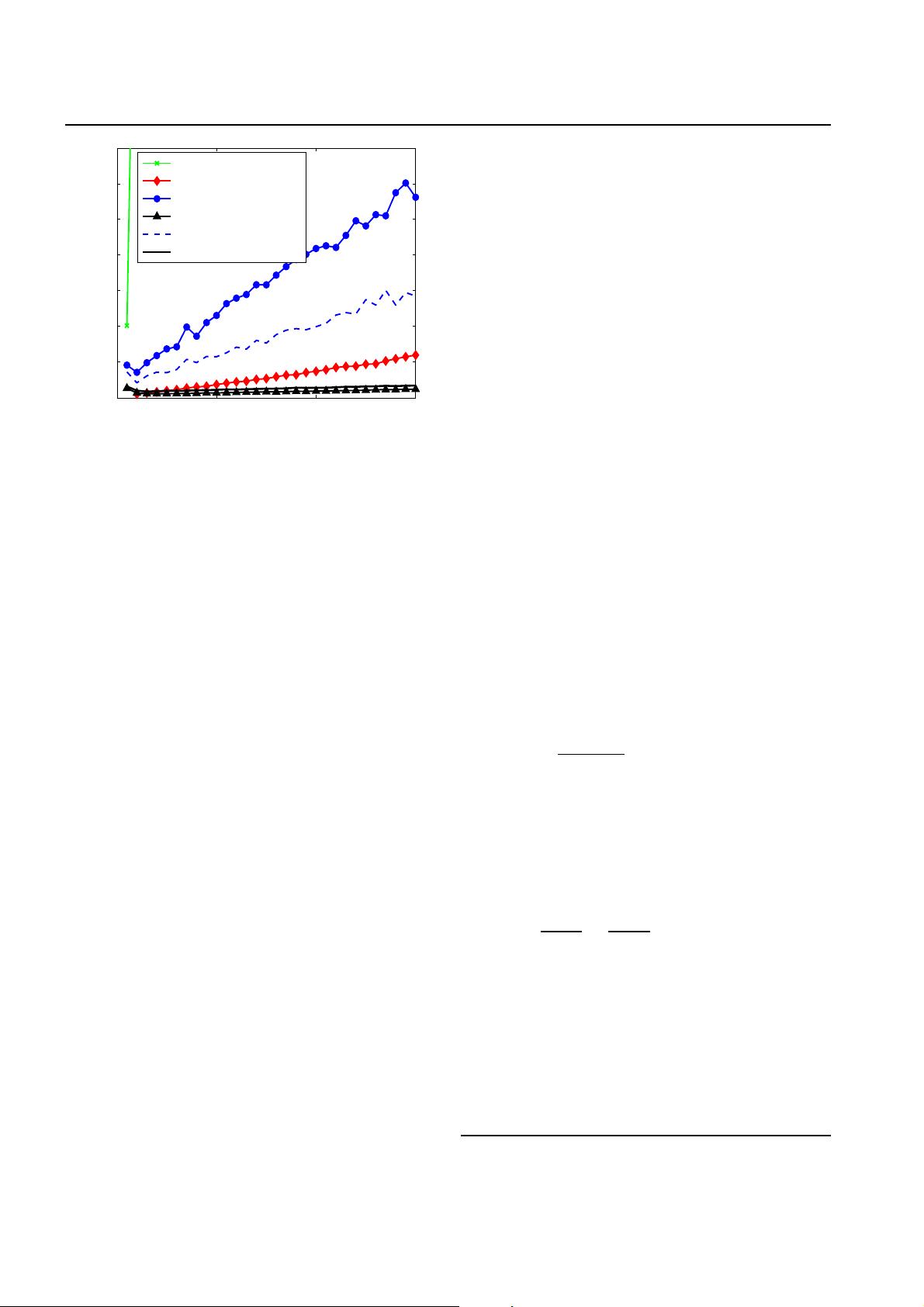
AD
Clamped DLT
LHM
EPnP
EPnP+LHM
EPnP+Gauss−Newton
Fig. 2 Comparing computation times of our method against the
state-of-the-art ones introduced in Fig. 1. The computation times
of a MATLAB implementation on a standard PC, are plotted
as a function of the number of correspondences. Our method
is both more accurate—see Fig. 1—and faster than the other
non-iterative ones, especially for large amounts of noise, and is
almost as accurate as the iterative LHM. Furthermore, if maximal
precision is required, the output of our algorithm can be used to
initialize a Gauss-Newton optimization procedure which requires
a negligible amount of additional time.
dinates of the control points in the camera referential,
which can be done in O(n) time by expressing these
coordinates as weighted sum of the eigenvectors of a
12 × 12 matrix and solving a small constant number
of quadratic equations to pick the right weights. Our
approach also extends to planar configurations, which
cause problems for some methods as discussed in [23,
25], by using three control points instead of four.
In the remainder of the paper, we first discuss re-
lated work focusing on accuracy and computational com-
plexity. We then introduce our new formulation and
derive our system of linear and quadratic equations.
Finally, we compare our method against the state-of-
the-art ones using synthetic data and demonstrate it
using real data. This paper is an expanded version of
that in [22], where a final Gauss-Newton optimization
is added to the original algorithm. In Section 4 we show
that optimizing over a reduced number of parameters,
the accuracy of the closed-solution proposed in [22] is
considerably improved with almost no additional com-
putational cost.
2 Related Work
There is an immense body of literature on pose estima-
tion from point correspondences and, here, we focus on
non-iterative approaches since our method falls in this
category. In addition, we will also introduce the Lu et
al. [20] iterative method, which yields very good results
and against which we compare our own approach.
Most of the non-iterative approaches, if not all of
them, proceed by first estimating the points 3D posi-
tions in the camera coordinate system by solving for
the points depths. It is then easy to retrieve the cam-
era position and orientation as the Euclidean motion
that aligns these positions on the given coordinates in
the world coordinate system [15,3,30].
The P3P case has been extensively studied in the lit-
erature, and many closed form solutions have been pro-
posed such as [6,8,9,11,24]. It typically involves solving
for the roots of an eight-degree polynomial with only
even terms, yielding up to four solutions in general, so
that a fourth point is needed for disambiguation. Fisher
and Bolles [8] reduced the P4P problem to the P3P one
by taking subsets of three points and checking consis-
tency. Similarly, Horaud et al. [13] reduced the P4P
to a 3-line problem. For the 4 and 5 points problem,
Triggs [29] derived a system of quadratic polynomials,
which solves using multiresultant theory. However, as
pointed out in [2], this does not perform well for larger
number of points.
Even if four correspondences are sufficient in gen-
eral to estimate the pose, it is nonetheless desirable
to consider larger point sets to introduce redundancy
and reduce the sensitivity to noise. To do so, Quan and
Lan [24] consider triplets of points and for each one
derive four-degree polynomials in the unknown point
depths. The coefficients of these polynomials are then
arranged in a
(n−1)(n−2)
2
× 5 matrix and singular value
decomposition (SVD) is used to estimate the unknown
depths. This method is repeated for all of the n points
and therefore involves O(n
5
) operations.
2
It should be
noted that, even if it is not done in [24], this complex-
ity could be reduced to O(n
3
) by applying the same
trick as we do when performing the SVD, but even
then, it would remain slower than our method. Ansar
and Daniilidis [2] derive a set of quadratic equations ar-
ranged in a
n(n−1)
2
×
n(n+1)
2
+1
linear system, which,
as formulated in the paper, requires O(n
8
) operations
to be solved. They show their approach performs better
than [24].
The complexity of the previous two approaches stems
from the fact that quadratic terms are introduced from
the inter-point distances constraints. The linearization
of these equations produces additional parameters, which
increase the complexity of the system. Fiore’s method [7]
avoids the need for these constraints: He initially forms
2
Following [10], we consider that the SVD for a m × n matrix
can be computed by a O(4m
2
n +8mn
2
+9n
3
) algorithm.









