消防救援策略研究:时间序列与多元线性回归
版权申诉
"这篇文档是2021年五一数学建模竞赛的参赛作品,主要研究消防救援问题,包括值班人员配置、出警次数预测、事件发生频率与月份的关系、事件密度与地理位置间的关系以及人口密度与事件密度的关联性,并通过规划模型确定消防站的选址。文档附带了程序代码,可供学习或教学使用。"
本文档深入探讨了消防救援领域的一系列关键问题,首先,针对问题一,研究者通过分析2016年至2020年特定时间段的出警次数,采用比例分配方法为30名消防员制定了值班计划。研究结果显示,每年2月1日、5月1日、8月1日、11月1日三个时间段的值班人数分别为5、12、13人;5、17、8人;5、12、13人;5、15、10人,以优化人力资源分配。
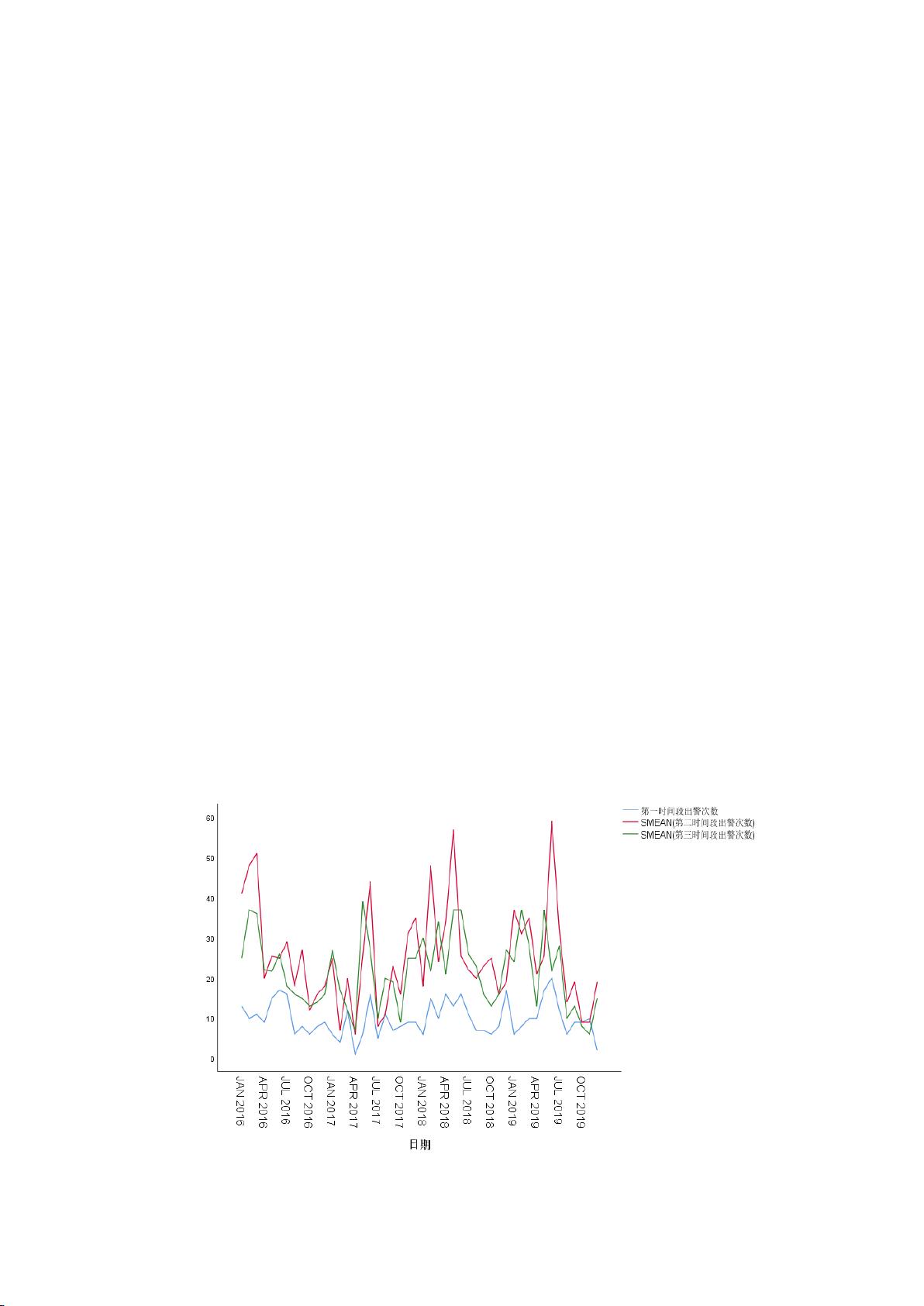
接着,对于问题二,建立时间序列模型并利用SPSS软件对2020年出警次数进行预测,验证模型的准确性后,预测2021年各月出警次数,预测值分别为56、58、60、43、73、68、46、37、41、29、41、52,为后续决策提供数据支持。
问题三关注的是事件发生与月份的关系。通过比较多元线性回归与非线性回归,发现多元线性回归分析的R方值更高,拟合效果更优,因此选择多元线性回归建立方程,表明各类型事件的发生次数与月份之间存在明确的线性关系。
在问题四中,运用Floyd算法和相关性分析,计算15个地区间的最短距离,并在SPSS中分析事件密度与这些距离的关系,识别出不同区域相关性最强的事件类别,具体结果记录在附录中。
问题五涉及人口密度与事件密度的关联性,通过对各类事件密度与人口密度进行相关性分析,得出两者之间存在极强的相关性,这为理解人口分布对火灾风险的影响提供了依据。
最后,在问题六中,建立了规划模型,结合Topsis熵权法和Matlab软件,计算各地区出警次数的权重和总最短距离的权重,以此确定最佳消防站位置。模型的目标是最小化平均出警距离,同时考虑出警次数的约束。
这篇论文通过严谨的数学建模和数据分析,为消防救援策略提供了科学依据,不仅适用于比赛,也具有很高的教学和实践价值。
相关推荐





maligebilaowang
- 粉丝: 6166
最新资源
- Java调用DLL方法详解:JNI与Jacob实战
- Microsoft的优质代码实践:编写无错C程序
- 正则表达式入门教程:掌握RegExp语法规则和用途
- 戴尔台式机报修指南:服务标签与故障诊断
- Dev-C++ 4.9.9.2 安装与基础操作指南
- Discuz! Rewrite规则全集:快速配置教程
- PDF制作指南:Adobe Acrobat 7.0 Professional打造电子书
- Java构造器与初始化清理
- SAP R/3全貌:90页中文详解与国内外成功与失败案例
- Oracle9i高级复制实施技巧与注意事项
- Java SCJP 1.4 认证考试题库:序列化和反序列化
- TreeView控件的高级用法:部门树结构与连锁选择
- ASP编程:Request与Response对象深度解析
- LoadRunner分析指南:理解与应用
- 深入理解EcmaScript:JavaScript与JScript之基础
- 《深入浅出MFC》2/e电子书开放下载