改进的MGOBA算法：多径衰落信道下块自适应DFE优化

需积分: 9 12 浏览量更新于2024-12-30 收藏 126KB PDF 举报

本文档主要探讨了一种新的改进型全局最优块自适应(MGOBA)算法，用于多径衰落信道下的块决策反馈均衡(DFE)。传统的全局最优块自适应算法(GOBA)专为处理实值信号设计，当块长度小于决策反馈均衡器系数的数量时，其递归过程可能无法正确工作。相比之下，MGOBA算法具有显著的创新性，它能够处理复值信号，并且其递归机制不受块长度和DFE系数数量的限制。作者Terence Wang和Chin-Liang Wang针对无线通信系统中的快速衰落射频通道提出了这个算法。与传统的基于序列卡尔曼滤波器的自适应方法以及先前提出的其他最优块自适应算法相比，MGOBA算法在块自适应DFE的性能上表现出色，尤其是在处理多径衰落带来的信号失真方面。它通过优化滤波器参数的自适应更新，提高了信号的恢复质量，从而降低了误码率。该算法的关键在于采用了块处理策略，将信号划分为固定大小的块进行处理，这在实时性和计算效率上具有一定优势。同时，MGOBA算法的设计考虑了复数域的运算，使得它不仅适用于无线通信系统，也可能扩展到其他需要复数信号处理的领域，如雷达和通信信号分析。总结来说，本文的工作在于提出了一种通用的自适应滤波技术，适用于多路径环境下的通信系统，特别是在处理快速变化的无线信号时，其优越的性能使得它在通信工程和信号处理领域具有广泛的应用潜力。对于研究者和工程师来说，这是一项值得深入研究和实践的技术，它有可能推动未来通信系统的性能提升和复杂环境下的信号传输优化。

IEEE TRANSACTIONS ON CIRCUITS AND SYSTEMS—II: ANALOG AND DIGITAL SIGNAL PROCESSING, VOL. 44, NO. 10, OCTOBER 1997 877

A New Block Adaptive Filtering Algorithm for

Decision-Feedback Equalization of Multipath

Fading Channels

Terence Wang and Chin-Liang Wang

Abstract—This brief presents a modiﬁed general optimum block adap-

tive (MGOBA) algorithm for block adaptive decision-feedback equal-

ization (DFE) of multipath fading channels. Unlike the original GOBA

algorithm, which was proposed only for processing real-valued signals

and its recursion cannot work correctly for adaptive DFE when the

block length is less than the number of decision-feedback equalizer (also

abbreviated to DFE) coefﬁcients, the MGOBA algorithm can process

complex-valued signals and its recursion has no constraints on the block

length as well as the number of DFE coefﬁcients. As compared to the

sequential Kalman and another previously proposed optimum block

adaptive algorithms, the MGOBA algorithm achieves better error-rate

performance for block adaptive DFE of rapidly fading radio channels.

Index Terms—Adaptive ﬁltering, block adaptive algorithm, decision-

feedback equalization, intersymbol interference, multipath fading chan-

nel.

I. INTRODUCTION

Radio channels are important communication links in modern

data transmission systems. Unlike telephone channels, whose im-

pulse responses are time-invariant or very slowly time-varying, radio

channels have randomly time-varying impulse responses caused by

several distinct independent propagation paths as well as continually

changing physical characteristics of the media [1]. Therefore, they

have been referred to as multipath fading channels.

Mitigation of intersymbol interference (ISI) from multipath fading

channels can be accomplished by decision-feedback equalization

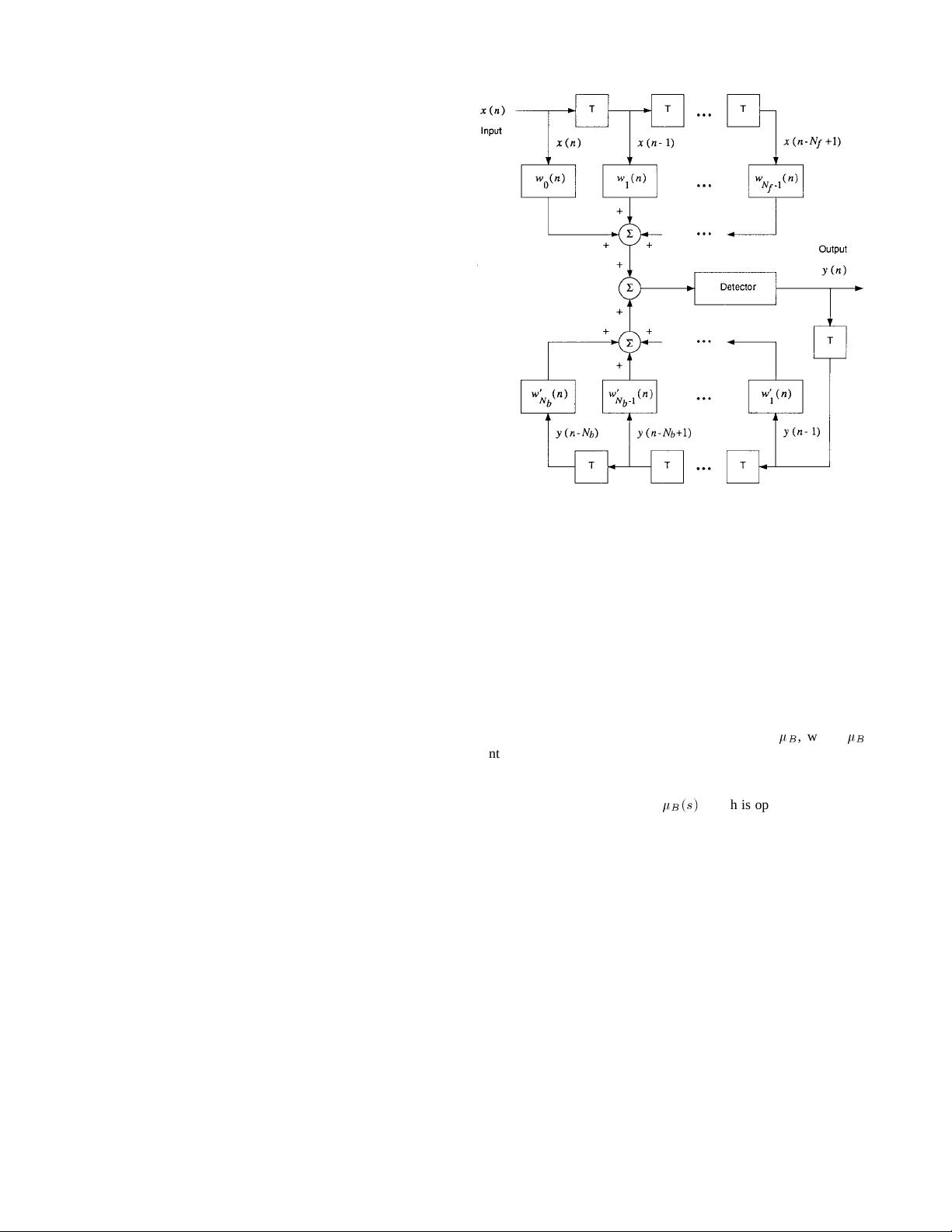
(DFE) [2]. Basically, a decision-feedback equalizer (also abbreviated

to DFE) consists of a feedforward ﬁlter, a feedback ﬁlter, and a

threshold detector as shown in Fig. 1. As compared to the maximum

likelihood sequence estimation (MLSE) technique [3], which is

optimum in the sense that the probability of a sequence error is

minimized, the DFE has much lower computational complexity and

could reach comparable performance on real recorded high frequency

(HF) channels [2]. A number of adaptive DFE methods have been

proposed for multipath fading channels, such as one-directional

equalization [4], bidirectional equalization [5], and block equalization

[6]. Among them, the one-directional and bidirectional approaches

involve the decision-directed mode where the DFE coefﬁcients are

adjusted using the threshold detector’s output. One major problem

associated with the decision-directed mode is that it may cause

divergence of the corresponding adaptive DFE system when the

channel has fast time variations and/or a deep fade. In contrast, the

block adaptive DFE approach updates the DFE coefﬁcients based

only on known training sequences and does not involve the decision-

directed mode; as a consequence, it avoids the serious divergence

problem and has much less average computational complexity.

To update the DFE coefﬁcients of a block adaptive DFE system,

a sequential or block adaptive algorithm can be used. A sequential

Manuscript received June 13, 1995; revised December 11, 1996. This paper

was recommended by Associate Editor T. Hinamoto.

The authors are with the Department of Electrical Engineering, Na-

tional Tsing Hua University, Hsinchu, Taiwan 30043, R.O.C. (e-mail:

clwang@ee.nthu.edu.tw).

Publisher Item Identiﬁer S 1057-7130(97)06585-3.

Fig. 1. The basic DFE structure.

adaptive algorithm adjusts the coefﬁcients when a new input data

sample arrives, while a block adaptive algorithm adjusts them only

once every block of input data samples. The sequential Kalman

algorithm [7], [8] has been shown to be useful for DFE of multipath

fading channels. However, it was indicated in [9] and [10] that a block

adaptive algorithm usually provides better tracking performance than

a sequential one. This means that it is worth developing a good block

adaptive algorithm for block adaptive DFE systems.

Some block adaptive algorithms have been introduced in the

literature for adaptive ﬁnite impulse response (FIR) ﬁltering. The

block least mean square (BLMS) algorithm in [9] is a stochastic

gradient algorithm with a ﬁxed convergence factor



, where



controls the convergence speed, accuracy, and stability of the adaptive

system. Unlike the BLMS algorithm, the optimum block adaptive

(OBA) and the OBA shifting (OBAS) algorithms [11] employ a

time-varying convergence factor



(

)

which is optimized in a least

squares (LS) sense and updated at each block iteration. Although

these two algorithms converge at higher rates than the BLMS algo-

rithm to achieve the same convergence accuracy, their convergence

rates deteriorate when the adaptive ﬁlter order is high and/or the

input signal is colored (band-limited) [11]. This problem can be

solved by using the block fast transversal ﬁlters (BFTF) algorithm

in [12] or the optimum block adaptive algorithm with individual

adaptation of parameters (OBAI) in [13]. These two algorithms were

derived based on LS criteria, and they may be said to be equivalent

since their estimates of the Wiener solution are the same at each

block iteration. This can be checked by comparing (7) and (16) in

[12] with (19) and (29) in [13]. The BFTF and OBAI algorithms

achieve better convergence and faster tracking than the BLMS and

OBA/OBAS algorithms when the block length is greater than or

equal to the FIR ﬁlter coefﬁcient number, but they do not work in

the opposite case [14]. In [14], a general optimum block adaptive

(GOBA) algorithm was proposed for adaptive FIR ﬁltering. For this

1057–7130/97$10.00  1997 IEEE

Authorized licensed use limited to: HARBIN ENGINEERING UNIV LIBRARY. Downloaded on March 30, 2009 at 08:41 from IEEE Xplore. Restrictions apply.

下载后可阅读完整内容，剩余4页未读，立即下载

xuehen2008

粉丝: 0
资源: 5

改进的MGOBA算法：多径衰落信道下块自适应DFE优化

Adaptive Filtering Primer with Matlab

Subband Adaptive Filtering Theory and Implementation

QRD-RLS Adaptive Filtering Jos´e Antonio Apolin´ario Jr.

subband adaptive filtering matlab代码

bad adaptive filter value

adaptive filtering algorithms and practical implementation

引用Distributed adaptive coverage control algorithm for mobile sensor networks

adaptive boosting algorithm 如何自己创建弱学习器

帮我写一个以蒙特卡洛方法为核心的若学习器adaptive boosting algorithm

design 3rd order Adaptive Torque Filter

最新资源