动态规划基础与应用：从数字三角形问题解析

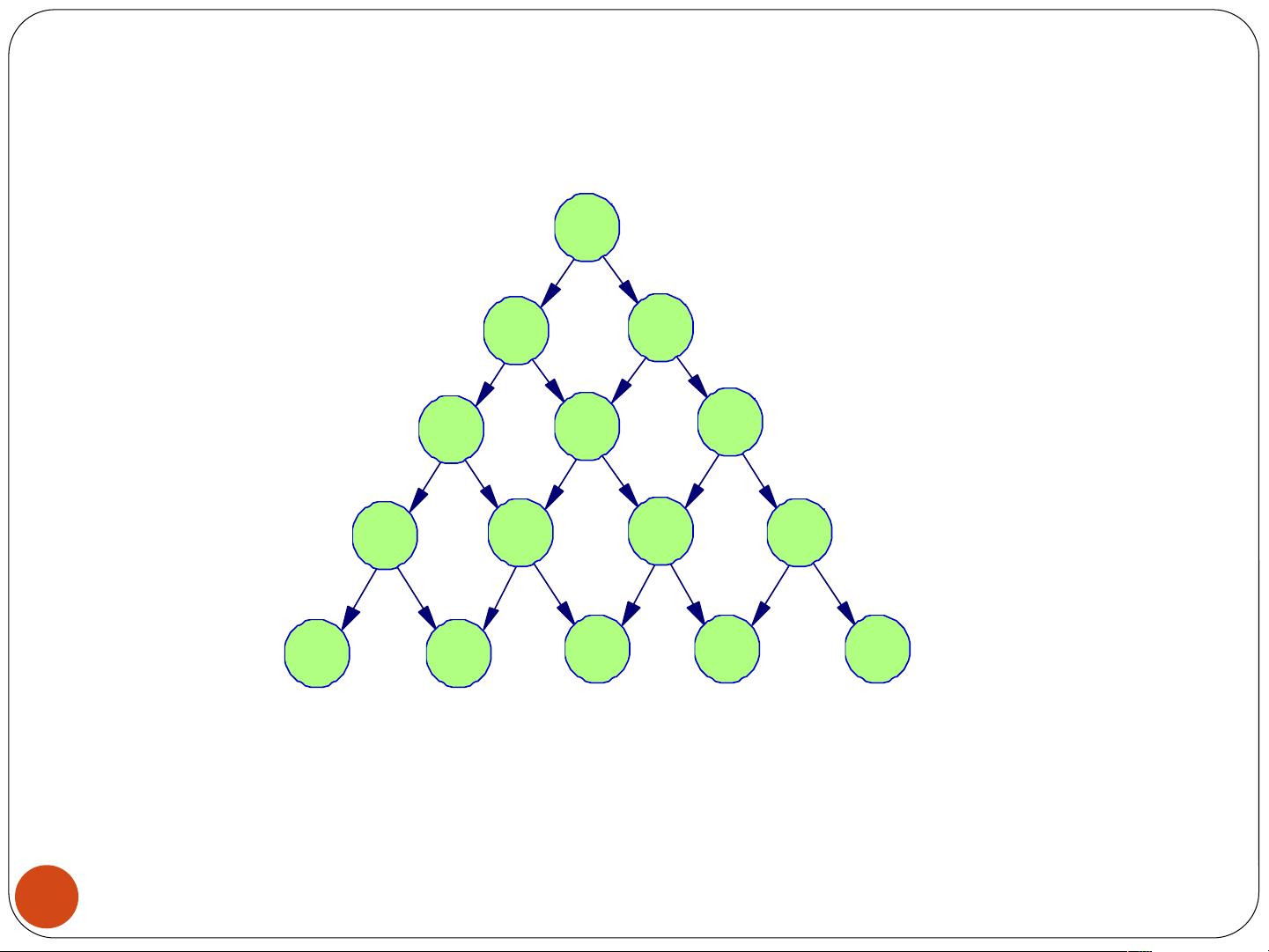
"该资料是关于动态规划算法的初步介绍，主要探讨了动态规划的基本概念、常见模型以及通过一个具体的数字三角形问题进行解析。动态规划是一种解决最优化问题的算法，它在信息学竞赛中被广泛考察，尤其在IOI、NOI和NOIP等竞赛中有着重要的地位。与常规算法不同，动态规划没有固定模式，需要深入理解问题并运用数学思维来构建解决方案。对于初学者来说，理解和掌握动态规划需要大量实践。文档中提到了数字三角形问题，这是一个典型的动态规划应用，要求找到从三角形顶部到底部，路径上数字之和最大的路径。这个问题可以通过深度优先搜索（DFS）策略来解决，但更常见的是使用动态规划的自底向上或自顶向下方法来优化解决方案。" 在动态规划的基本概念部分，通常会讲解如何通过定义状态、状态转移方程以及边界条件来构建问题的解决方案。状态通常是问题的关键属性，而状态转移方程描述了从一个状态到另一个状态的转换过程。在数字三角形问题中，状态可以是到达某一行某一列的路径和，状态转移方程则是根据当前状态和相邻的状态来计算下一个状态的路径和。 接着，文档可能会介绍动态规划的常见模型，如最长公共子序列、背包问题、最短路径问题等，这些都是动态规划的经典应用。通过这些模型，学习者可以更好地理解和运用动态规划的思想。 对于数字三角形问题，虽然可以用深度优先搜索来解决，但效率较低，更适合的解决方案是使用动态规划数组。自底向上地填充数组，每一层的元素基于下一层的元素计算得出，这样避免了重复计算，提高了效率。在这个例子中，可以创建一个二维数组dp，其中dp[i][j]表示到达第i行第j列的最大路径和。通过迭代，从第二行开始，根据下一行的两个相邻元素来更新当前行的最大路径和。 最后，文档可能还会强调，掌握动态规划不仅仅是学会编写代码，更重要的是理解问题的内在结构，形成正确的思维模式，这将有助于解决更复杂的问题。动态规划的精髓在于分解问题，找出最优子结构，并通过重用子问题的解来避免重复计算，从而达到全局最优。因此，通过不断地练习和分析，才能真正掌握动态规划这一强大的算法工具。