线性代数基础:3blue1brown线性代数系列视频课程笔记
需积分: 0 110 浏览量
更新于2024-02-02
1
收藏 762KB PDF 举报
本文是基于3blue1brown线性代数系列视频课程的笔记,所有内容均来自3blue1brown。在这个视频系列中,我们将会学习线性代数的基础知识。
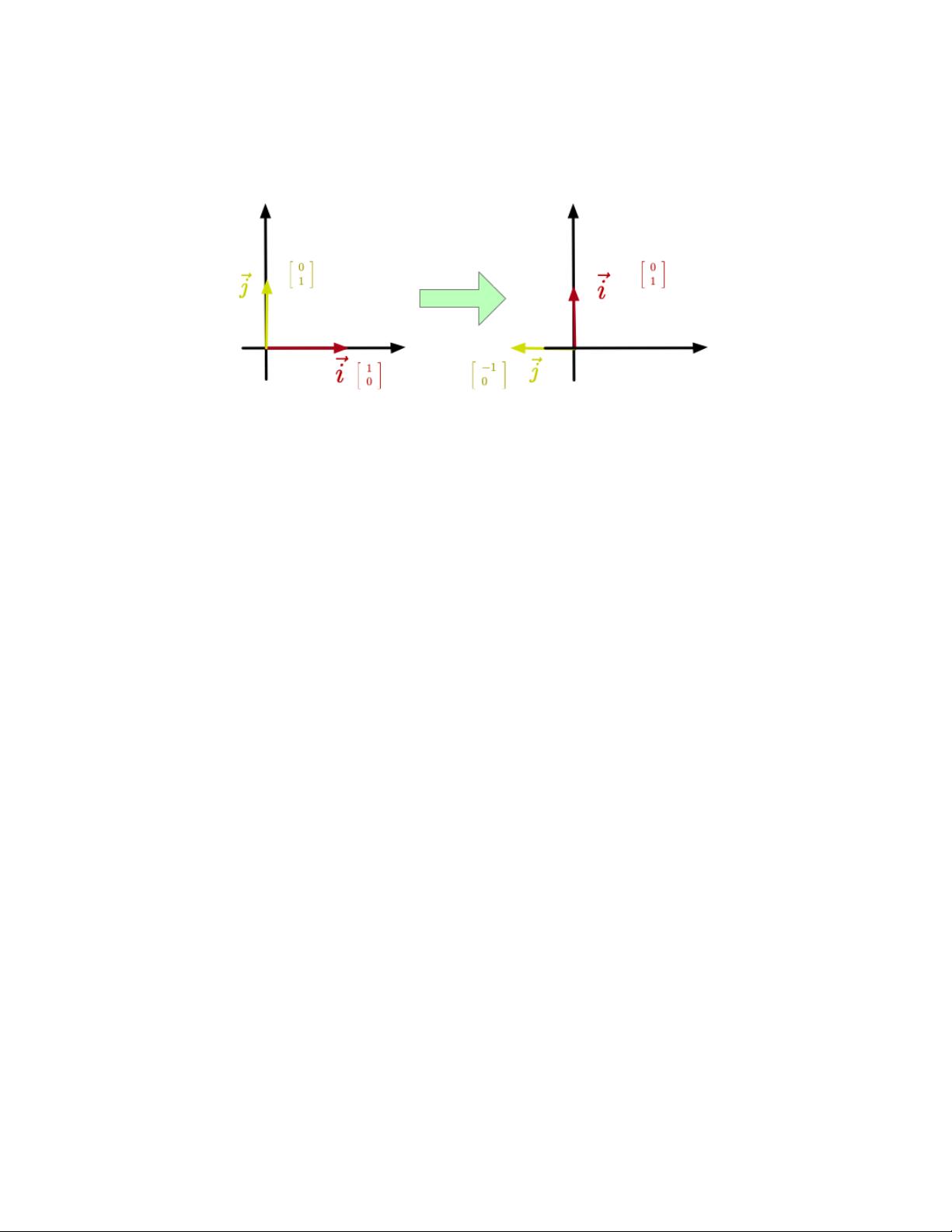
线性代数是数学中的一个分支,主要研究向量空间和线性映射。在物理学中,向量经常被看作空间中的一个箭头,表示位置、速度、加速度等物理量。而在线性代数中,向量是由若干个标量组成的有序集合,可以表示为一个列向量。
在线性代数中,我们将学习向量的加法和数量乘法运算,以及向量空间的基本性质。向量的加法是将两个向量的对应分量相加,数量乘法是将向量的每个分量与一个实数相乘。通过这些运算,我们可以定义向量空间,并且可以在向量空间中进行代数运算和向量之间的关系运算。
我们还将学习向量的线性组合和线性相关的概念。线性组合是指将若干个向量与对应的实数进行数量乘法和加法运算得到的新的向量。线性相关是指如果存在一个向量的线性组合等于零向量,则这些向量是线性相关的。通过线性组合和线性相关的概念,我们可以判断向量集合的线性无关性和生成空间。
在线性代数中,我们还将学习矩阵和线性方程组的相关知识。矩阵是由若干个数构成的矩形阵列,可以表示线性变换和线性方程组。线性方程组是一组线性方程的集合,其中未知数的常系数构成了一个矩阵,通过求解矩阵方程,我们可以确定线性方程组的解。
最后,我们将学习矩阵的逆和行列式的概念。矩阵的逆是指存在一个矩阵,使得该矩阵与原矩阵相乘得到单位矩阵。行列式是一个数值,可以表示矩阵的某些性质,例如是否可逆、奇偶性等。
通过学习线性代数的基础知识,我们可以更好地理解和描述物理学中的向量和线性方程组。线性代数在数学、工程、计算机科学等领域都有广泛的应用,是一门非常重要的学科。
总而言之,3blue1brown线性代数系列视频课程为我们提供了线性代数的基础知识,包括向量视角、向量运算、线性相关、矩阵和线性方程组等内容。通过学习线性代数,我们可以更好地理解和描述物理学中的向量和线性方程组,在各个领域中得到应用。
2022-08-03 上传
250 浏览量
232 浏览量
132 浏览量
132 浏览量
271 浏览量
144 浏览量
362 浏览量
SeaNico
- 粉丝: 26

最新资源
- XMLBBS在线论坛用户权限及操作指南
- Memcached 安装与服务程序快速部署指南
- 轻松实现Java操作MySQL数据库的jar包
- 5053线修复与系统升级指南
- Fun Race 3D游戏开发细节与改进策略
- RPGViewer工具包 - 游戏开发资源压缩包
- 最土仿糯米网优惠券插件v2.0安装与使用指南
- MinGW环境下Symbolic C++ 3的静态编译与实例
- 深入理解Visual Basic .NET中的TCPIP与Internet编程技术
- 文本选择器:正则表达式与xpath测试工具
- C#开发的RS232串口通信程序及新手指南
- CSS3实现Tilt-Shift效果的图像过滤器技巧
- CAD字体汇总:完整版2011年138个字体包
- ORL数据库:无需预处理的人脸识别图像与数据集
- Android视频采集与H264编码技术解析
- CJ-BOT:JavaScript技术实现的智能机器人