FIR数字滤波器设计方法与实现

"本文主要介绍了FIR数字滤波器的设计，包括其结构原理、线性相位特性以及设计方法，如窗函数法。" 在数字信号处理领域，FIR（Finite Impulse Response，有限冲激响应）数字滤波器是一种广泛应用的滤波器类型。它们在信号预处理、防混叠、带通选择、抽取/插补、滤波和视频处理等场景中发挥着重要作用。FIR滤波器的主要特点是其输出只取决于当前和过去的输入样本，因此它们是稳定的。 FIR滤波器的传递函数通常表示为离散时间Z变换的形式，如公式(11-1)所示，其中N为滤波器阶数。系统差分方程(11-2)描述了滤波器如何通过线性卷积处理输入序列x(n)。直接型结构，如图11-2所示，是最常见的实现方式，它直观地展示了滤波器如何根据过去N-1个输入样本计算当前输出。 当滤波器的单位冲击响应h(n)具有对称性，即满足条件(11-3)，FIR滤波器将具有严格的线性相位特性。这在许多应用中是理想的，因为线性相位意味着滤波不会引入额外的相位失真。对于偶数阶的滤波器，其结构可以简化为式(11-4)和图11-3所示；对于奇数阶，结构如式(11-6)和图11-4所示。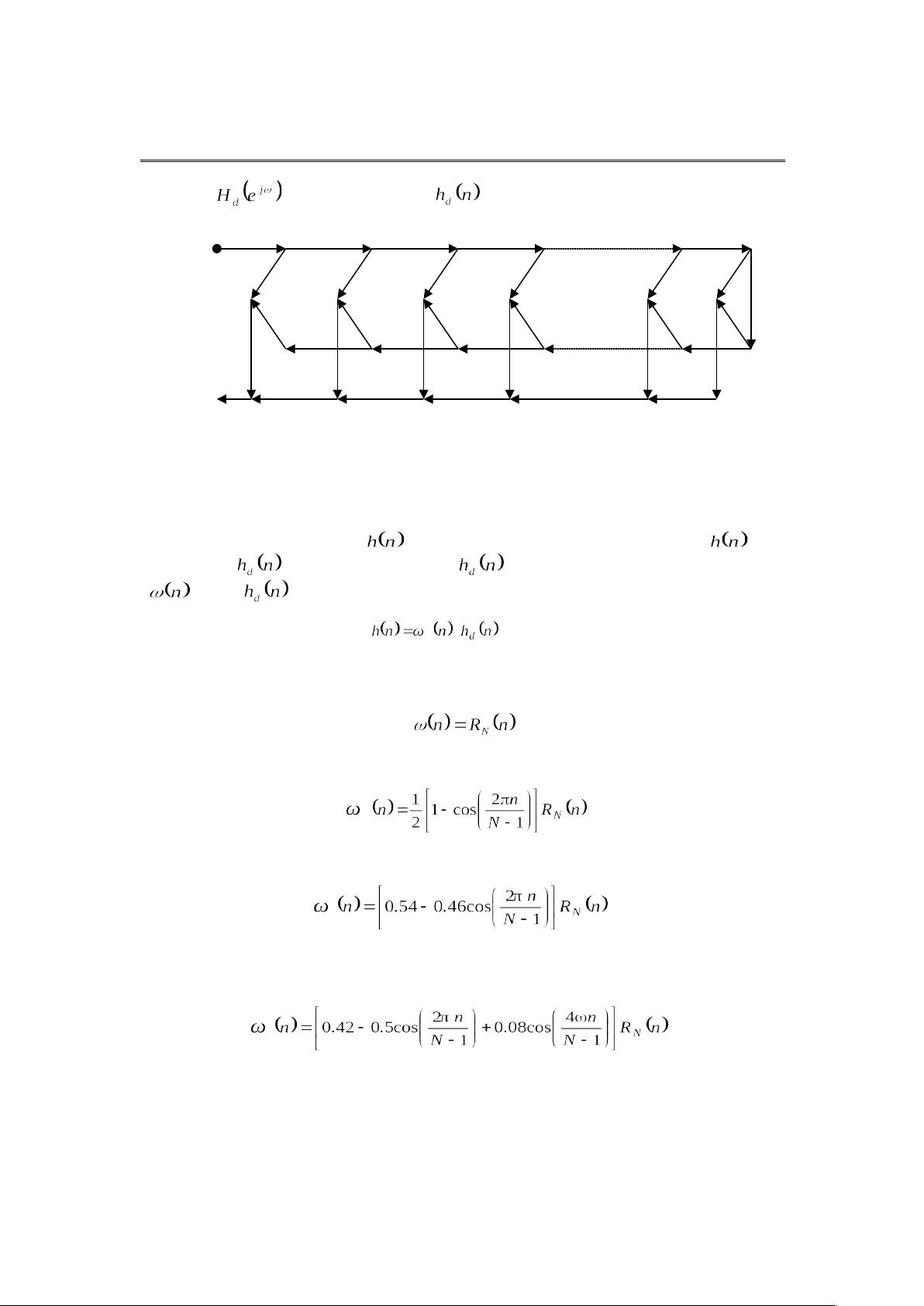 设计FIR滤波器有多种方法，其中包括窗函数法、频率取样法和等波纹优化设计法。窗函数法是其中最简单的方法，它涉及将理想频率响应Hd(e^(jω))转换到时域，然后通过截断或应用窗口函数来获得有限长的h(n)。窗口函数的选择影响滤波器的性能，例如矩形窗、汉宁窗和海明窗等。这些窗口函数在减少旁瓣幅度和控制过渡带宽度方面各有优缺点。 1. 矩形窗是最简单的窗口函数，但可能导致较高的旁瓣水平。 2. 汉宁窗（Hanning Window）在降低旁瓣的同时引入了主瓣的展宽。 3. 海明窗（Hamming Window），又称升余弦窗，进一步改进了汉宁窗，能提供更好的旁瓣抑制效果。 通过调整窗口函数的形状和长度，可以优化FIR滤波器的频率响应，以更好地匹配所需的理想滤波特性。FIR滤波器设计是一个平衡滤波器性能和计算复杂度的过程，适用于各种硬件平台，如CPLD（复杂可编程逻辑器件）和FPGA（现场可编程门阵列）实现。