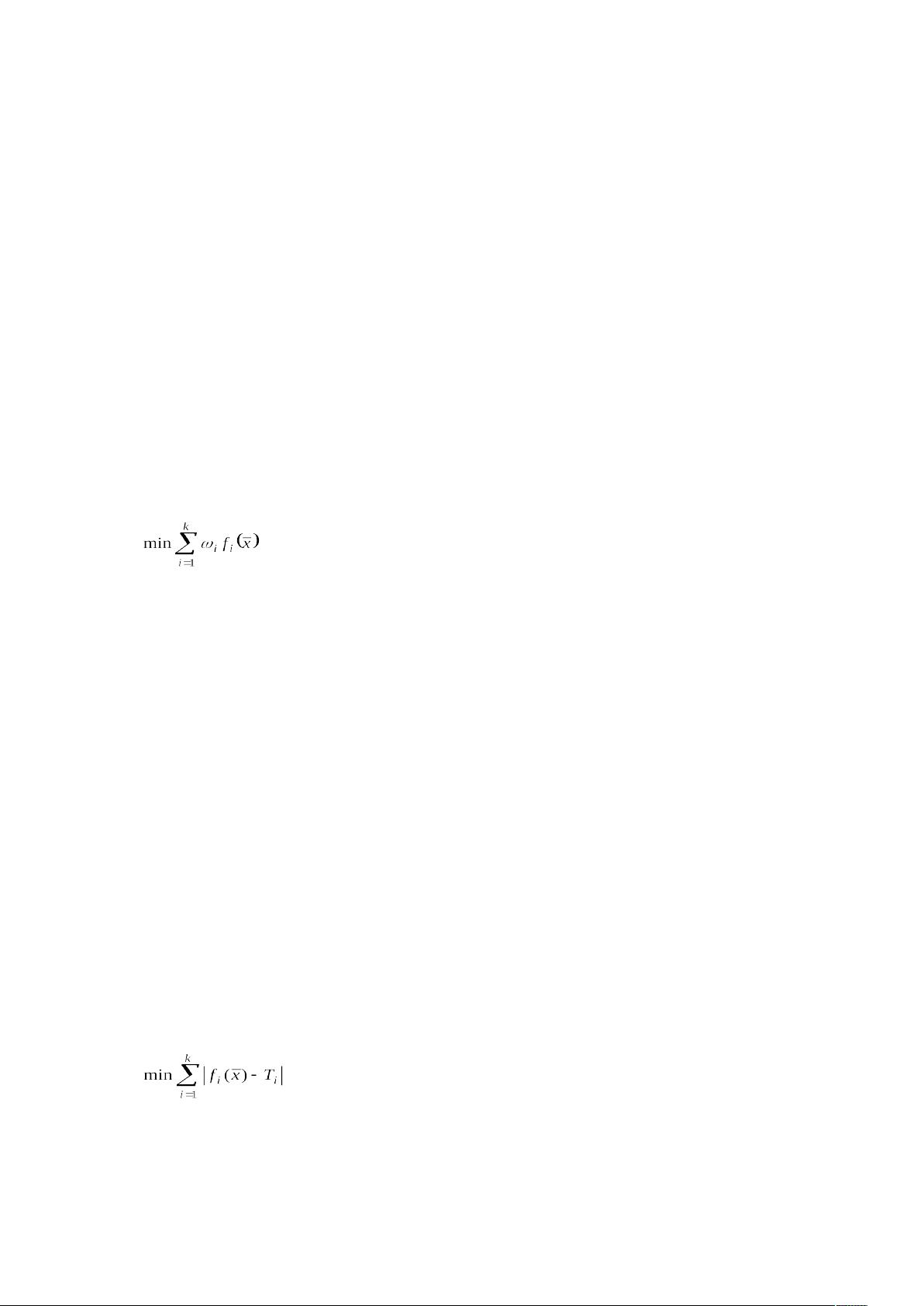遗传算法在多目标优化中的策略探讨

"本文探讨了遗传算法在解决多目标问题中的应用方法，主要涉及两种策略：权重法和目标规划法。" 遗传算法是一种基于生物进化原理的优化方法，它通过模拟自然选择和遗传机制来搜索解决方案空间。在多目标优化问题中，遗传算法需要将多个目标函数转换为单个适应度函数以便进行计算。常见的方法是将目标函数通过加权、乘法或其他数学手段综合成单一目标。然而，这种综合方法面临挑战，因为它要求对每个目标函数的取值范围有精确了解，以免某个目标函数的优势压倒其他函数。此外，这种方法可能导致高昂的计算成本，特别是在实际问题中。 1. 权重法 权重法是将每个目标函数乘以相应的权重，然后求和得到单一目标。权重的选择通常依赖于问题背景和决策者的偏好。由于权重的选择直接影响最终解的质量，而合适的权重往往难以确定，因此通常需要尝试多种权重组合，形成一个非劣解集合，由决策者根据需求选取最佳解。权重法的优点在于其计算效率，能快速产生非劣解。然而，如果没有足够的问题信息，确定权重系数可能很困难，导致找到的最优解依赖于权重设置，可能会丢失某些重要解。 2. 目标规划法 目标规划法源于线性目标规划，它允许决策者设定每个目标函数的理想或可接受值，并将这些值作为额外约束加入到优化问题中。基本思想是最小化目标函数与理想值之间的差距。这种方法使得决策者可以明确表达目标期望，但需要额外的工作来定义和调整目标值，且可能不适用于非线性或多维度的问题。 总结来说，遗传算法在处理多目标问题时，面临将多目标转换为单目标适应度函数的挑战。权重法和目标规划法是两种常用策略，各有优缺点。权重法高效但权重选择困难，目标规划法则更注重决策者的目标设定，但可能受到线性模型限制。在实际应用中，需要根据问题的具体情况和可用信息灵活选择合适的方法。同时，为了提高优化效果，可能还需要结合其他策略，如帕累托优化或纳什均衡等。