机器学习损失函数解析：MSE与MAE

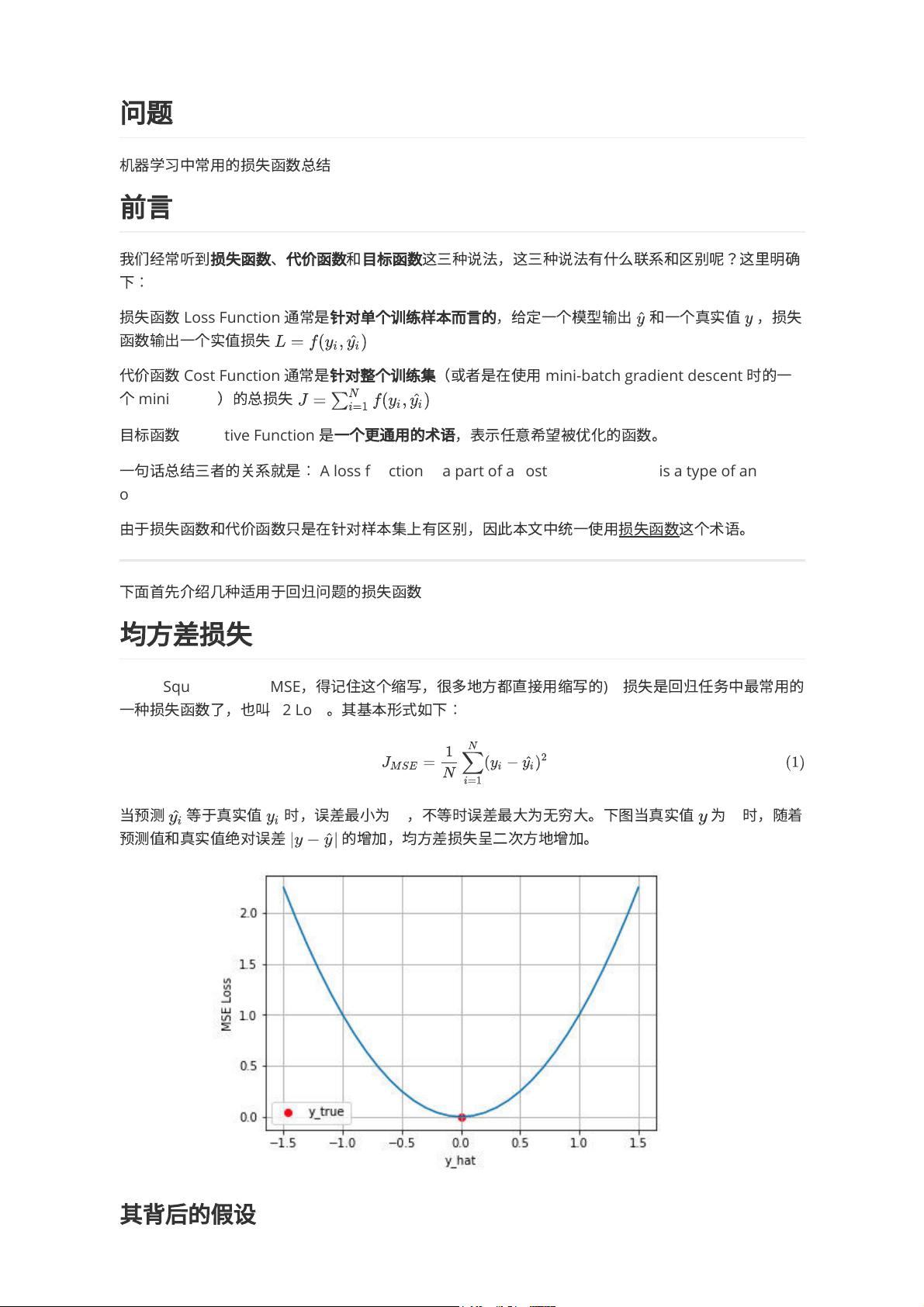
"这篇内容主要介绍了机器学习中常用的损失函数，包括它们的概念、关系以及在不同问题中的适用性。" 在机器学习中，损失函数、代价函数和目标函数是优化过程中的核心概念。损失函数（Loss Function）是衡量单个样本预测结果与实际值差异的度量，它给出的是模型输出与真实值之间的偏差。代价函数（Cost Function）是所有样本损失的总和，用于评估整个训练集或小批量样本的性能。目标函数（Objective Function）是一个更为通用的术语，可以表示任何需要被优化的函数，它可能包括损失函数和其他正则化项。 本文主要讨论了几种常见的回归问题损失函数： 1. 均方差损失（MSE，Mean Squared Error）：也称为L2 Loss，是最常见的回归问题损失函数。它的计算公式是预测值与真实值差的平方的平均值。MSE倾向于惩罚远离真实值的大误差，因为它是平方项，所以误差越大，损失增加的速度越快。当误差服从高斯分布时，最小化MSE损失函数等同于最大似然估计，使得它在回归问题中表现良好。但在分类问题中，由于误差不是离散的，MSE可能不是一个理想的损失函数。 2. 平均绝对误差损失（MAE，Mean Absolute Error）：也被称作L1 Loss，是预测值与真实值之差的绝对值的平均。与MSE相比，MAE对异常值的敏感度较低，因为它不是平方项，所以即使存在大误差，损失也不会无限增加。这种特性使得MAE在处理噪声较大或有离群值的数据时更加稳健。 除了这些，还有其他类型的损失函数，如对数损失（Log Loss）、Huber损失、绝对百分比误差损失（MAPE）等，适用于不同的问题。例如，对数损失通常用于二分类或多分类问题，因为它与交叉熵损失相关，能够更好地捕捉概率预测的准确性。而Huber损失结合了MSE和MAE的优点，对于小误差近似于MSE，而对于大误差接近MAE，因此在噪声和异常值共存的数据中表现出较好的鲁棒性。 在实际应用中，选择合适的损失函数对模型的性能至关重要。不同的损失函数对应着不同的优化目标和数据特性，理解并正确选择损失函数是构建高效机器学习模型的关键步骤。在实践中，还可以根据问题的具体需求，通过调整损失函数的参数或设计自定义损失函数来进一步优化模型。