并行Alpha-Beta剪枝算法的性能比较：Fail-Soft方法研究
177 浏览量
更新于2024-08-03
收藏 281KB PDF 举报
本篇论文深入探讨了并行Alpha-Beta剪枝在不同架构下的性能比较，特别是在五子棋AI（五子棋人工智能）搜索策略优化中的应用。随着计算机系统对高效搜索算法的需求增长，尤其是在实时操作中寻找最优解决方案时，减少计算时间成为关键问题。传统的minimax算法通过遍历所有可能的状态，构建完整的状态搜索空间，但其时间复杂性可能过于庞大，不适合实时应用场景。
Alpha-Beta剪枝作为一种实用的优化方法，旨在避免搜索整个状态空间，而是通过剪去不必要的分支来降低计算负担。这种方法的核心思想是在搜索过程中，通过评估当前节点的上下文，即环境状态、系统目标等，提前预测哪些路径不可能产生最好的结果，从而停止搜索这些分支，显著节省计算资源。
本文主要关注以下几个方面：
1. **并行Alpha-Beta剪枝技术**：研究者比较了不同架构（如多线程、分布式或GPU加速）下并行Alpha-Beta剪枝的效率和性能提升。不同的硬件和并行策略可能导致剪枝效果和搜索速度的变化，这在实际五子棋AI系统中具有重要意义。
2. **搜索空间的剪枝策略**：论文详细探讨了各种剪枝策略，包括基于先验知识的剪枝、启发式评估函数以及深度优先搜索与广度优先搜索的结合，这些都直接影响到搜索效率。
3. **算法的可扩展性和适应性**：论文分析了如何在保持算法效率的同时，使其能够适应不断变化的游戏环境和对手策略，这对于动态游戏环境下的AI至关重要。
4. **实验设计与评估**：通过精心设计的实验，作者定量地评估了不同实现方式下的性能，包括搜索速度、内存消耗和最终的决策质量，以便于确定最佳的剪枝策略。
5. **应用与未来方向**：论文不仅提供了当前并行Alpha-Beta剪枝在五子棋AI中的应用案例，还讨论了潜在的未来研究方向，如结合机器学习改进剪枝策略，或者将这种方法扩展到其他复杂决策问题。
这篇论文为理解和优化五子棋AI中的搜索算法提供了一种实用且有效的解决方案，有助于提高系统的响应速度和整体性能，对于追求高效计算和智能决策的现代AI系统开发具有重要的参考价值。
Comparative study of performance of parallel Alpha
Beta Pruning for different architectures
Shubhendra Pal Singhal
Department of Computer Science and Engineering
National Institute of Technology, Tiruchirappalli
shubhendrapalsinghal@gmail.com
M. Sridevi
Department of Computer Science and Engineering
National Institute of Technology, Tiruchirappalli
msridevi@nitt.edu
Abstract—Optimization of searching the best possible action
depending on various states like state of environment, system
goal etc. has been a major area of study in computer systems.
In any search algorithm, searching best possible solution from
the pool of every possibility known can lead to the construction
of the whole state search space popularly called as minimax
algorithm. This may lead to a impractical time complexities
which may not be suitable for real time searching operations.
One of the practical solution for the reduction in computational
time is Alpha Beta pruning. Instead of searching for the whole
state space, we prune the unnecessary branches, which helps
reduce the time by significant amount. This paper focuses on
the various possible implementations of the Alpha Beta pruning
algorithms and gives an insight of what algorithm can be used
for parallelism. Various studies have been conducted on how
to make Alpha Beta pruning faster. Parallelizing Alpha Beta
pruning for the GPUs specific architectures like mesh(CUDA)
etc. or shared memory model(OpenMP) helps in the reduction
of the computational time. This paper studies the comparison
between sequential and different parallel forms of Alpha Beta
pruning and their respective efficiency for the chess game as an
application.
Index Terms—Parallel algorithms, Minimax, Alpha Beta prun-
ing, CUDA, OpenMP, Mesh architecture, Shared memory model
I. INTRODUCTION
Playing a game strategically requires an individual to fore-
see all kinds of winning possibilities. The grading policy
applied to game tree is generally +1 for winning and -1
for losing which ultimately helps the agent decide the next
move. This may require the construction of whole state space
implying that every possibility or action needs to be considered
and whatever suits the best or takes the agent close to its goal,
should be opted. Now, this is the general brute force method
which might work practically for simpler and smaller games
like Tic-Tac-toe, but the complex games like checkers or chess
on 8*8 board, has a gigantic state space and searching using
the brute force method in such a huge space is impractical.
This gives us the motivation to study a better and feasible
method called Alpha Beta pruning. The cases which turns
out to be futile at the start of the search are rejected, thus
reducing the state space for every move by significant amount.
Furthermore, the efficiency of the Alpha Beta pruning can be
further improved, to suit feasibility of running AI applications
[1] consisting of accrued state space. Parallelism turns out
to be one of the factors which can be used to improve
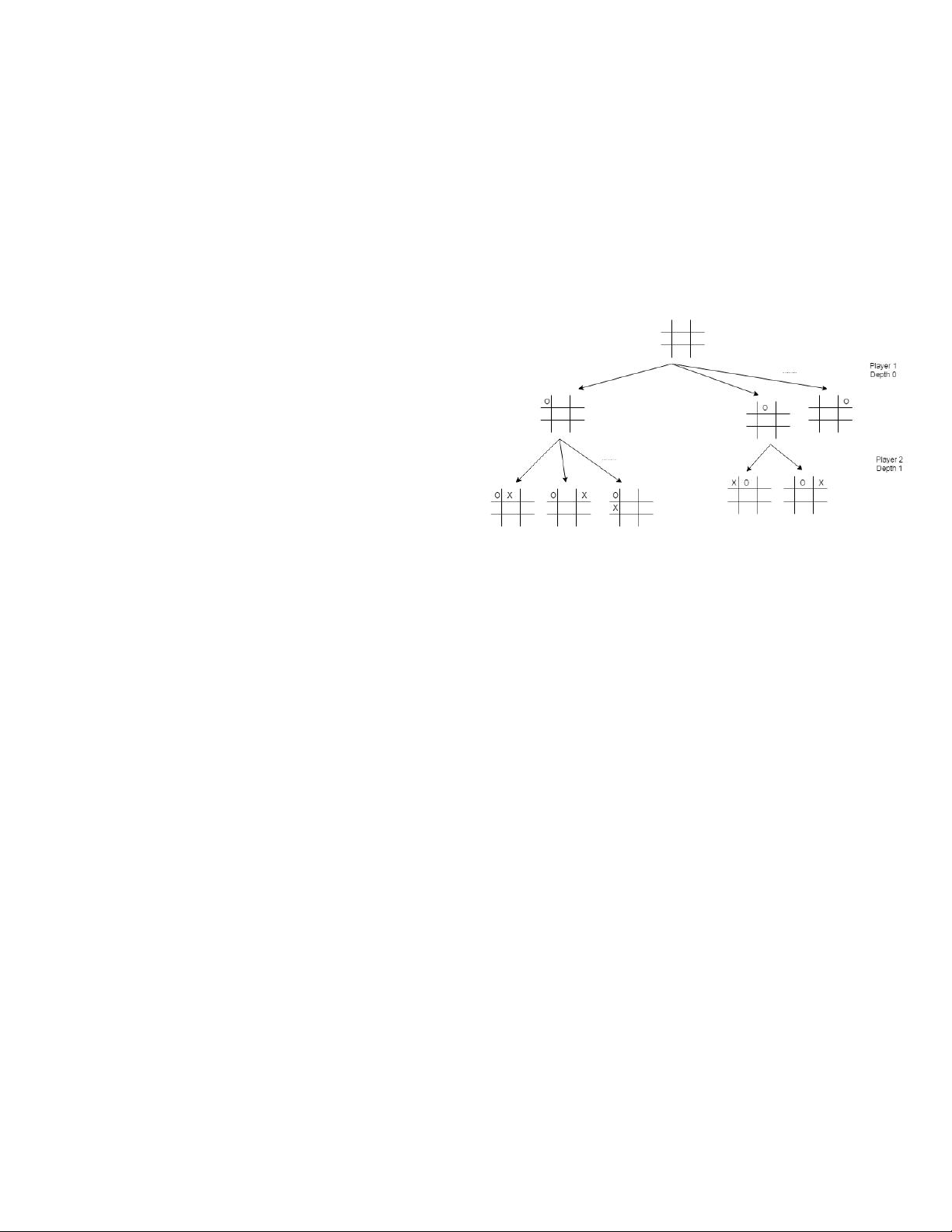
Fig. 1: Game tree for Tic-Tac-toe
the performance. This paper compares the performances and
speedup obtained from various implementations of the parallel
forms of Alpha Beta pruning on different architectures.
The earlier the branches are pruned, the better is the effi-
ciency of Alpha Beta pruning. Different architectures prune
the branches at different time stamps, thus differing in the
computation time.
A. Minimax Algorithm
Brute force search in the state space is the minimax
algorithm. Minimax is a decision-making algorithm [2]. The
main aim of the algorithm is to find the next best move as
shown in Fig1 for the game Tic-Tac-Toe [3] (application of
minimax) .
In the applications of Minimax algorithm (involving two
players), first player is maximizer, and the second player is
the minimizer. The evaluation score is assigned to the game
board, where the maximizer and minimizer aims to get the
highest score, and the lowest score possible respectively [2].
The implementation of the same in shown in the following
algorithm 1 [4].
If every child branch is allocated to one processor and
run the same algorithm in parallel for every child branch,
then the parallel minimax is formed. The parent child will
collect the answer from all the child branches and further
arXiv:1908.11660v2 [cs.DC] 29 Oct 2019
下载后可阅读完整内容，剩余4页未读，立即下载
2021-08-15 上传
2022-07-12 上传
2020-12-21 上传
2021-04-18 上传
2019-03-17 上传
2021-04-03 上传
2013-03-07 上传
2019-08-29 上传
2019-08-29 上传
BrokenGeeker
- 粉丝: 926
- 资源: 5
我的内容管理
展开
