MATLAB实现高斯分布聚类分析

"这篇资源是关于在MATLAB中进行聚类分析的代码示例，主要涉及高斯分布数据的生成和聚类算法的应用。通过随机生成服从不同高斯分布的样本，然后使用k-means算法进行两类聚类，并进一步展示了层次聚类的方法。" 在MATLAB中进行聚类分析是一项常见的任务，特别是在数据挖掘和机器学习领域。在这个例子中，首先通过高斯分布（正态分布）随机生成数据，随后应用k-means聚类算法以及层次聚类方法。 首先，我们来看数据生成部分。代码使用`rng`函数设置随机数种子，确保每次运行都能得到相同的结果。接着，通过`rand`函数生成3个中心点（`mu`）和对应的标准差（`sigma`）。这些中心点和标准差用于构建3个不同的高斯分布。然后，使用`mvnrnd`函数从这些分布中生成样本点，分别分配到3个类别中，每个类别具有不同数量的样本。 `mvnrnd(mu, SIGMA, N)`函数在MATLAB中用于生成多维正态分布的随机数，其中`mu`是期望向量，`SIGMA`是协方差矩阵，`N`是需要生成的样本数量。在这个例子中，每个类别都有不同的均值和标准差，使得数据分布在空间中有所区分。 接下来是聚类分析部分。`kmeans`函数用于执行k-means聚类。`kmeans(X, k, 'dist', 'sqEuclidean')`将输入数据`X`划分为`k`个类别，使用平方欧几里得距离作为距离度量。返回的`cidx2`是每个样本的类别标签，`cmeans2`是聚类中心，`sumd2`是每个点到其最近聚类中心的平方和，`D2`是所有点的距离矩阵。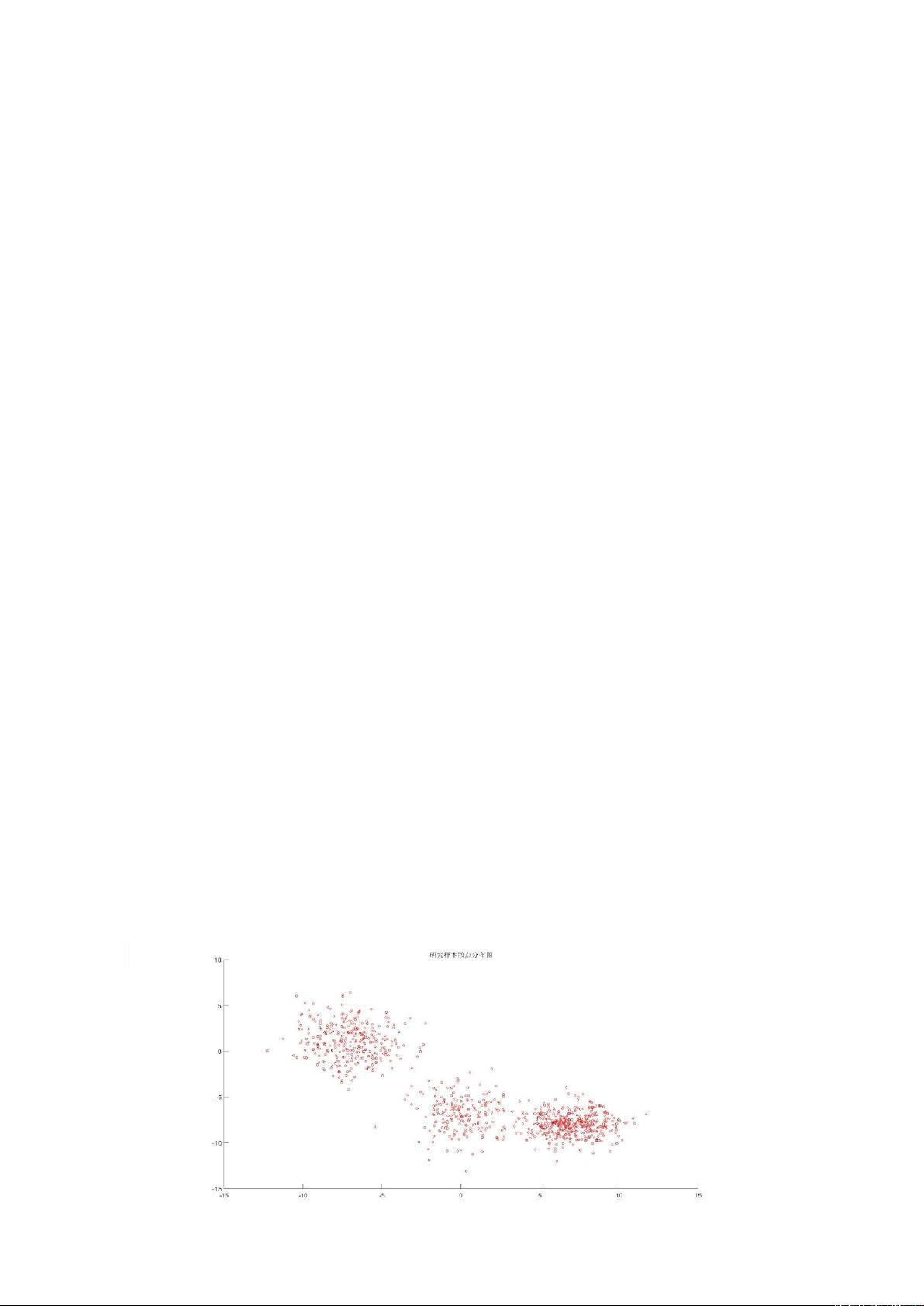 为了可视化结果，`scatter`函数用于绘制研究样本的散点图，而`silhouette`函数则用于计算轮廓系数，帮助评估聚类效果。轮廓系数可以衡量一个样本点属于当前聚类的紧密程度与属于其他聚类的松散程度，有助于理解聚类的合理性。 最后，代码演示了层次聚类。`pdist`函数计算所有样本之间的欧式距离，`linkage`函数基于这些距离生成层次聚类树，这里采用的是平均链接（'average'）方法。`cophenet`函数则计算一致性系数，用于评价层次聚类的质量。 通过这个代码，我们可以学习如何在MATLAB中创建高斯分布的数据集，以及如何应用k-means和层次聚类算法进行聚类分析。这不仅是一个理论知识的实践，也是对MATLAB编程能力的锻炼。在实际应用中，这些技能对于理解和处理复杂数据集至关重要。