Smith圆图解析：微波器件设计的关键工具

"微波基础知识-smith圆图详解" Smith圆图是微波工程中用于分析和设计微波网络的一种重要工具，特别是在处理反射系数、阻抗匹配等问题时显得尤为实用。它通过图形化的方式，使得阻抗和反射系数之间的关系变得直观易懂。 Smith圆图的基本构成基于反射系数Γ，其数学表达式为Γ = (z - 1) / (z + 1)，其中z是复数形式的阻抗，通常表示为 z = r * exp(jθ)，其中r是反射系数的模，θ是相位角。Smith圆图上，|Γ|的大小表示在无耗传输线中的反射程度，是一个不变量，而Γ的相位θ则表示反射相位。 Smith圆图上的关键点包括电压驻波比ρ的轨迹。在圆图上，电压波腹点（即电压最大值处）的轨迹对应于电压驻波比ρ的值，这可以用来评估系统匹配程度。例如，当Γ位于正实轴时，对应的电阻值就是ρ的值。A点表示负载的反射系数，B点则表示传输线上电压波腹点的反射系数，且B点的电阻值等于电压驻波比ρ。 此外，Smith圆图还包括了导纳圆图，它可以同时处理阻抗和导纳问题，具有两套刻度，可以直接读出导纳值。通过简单的操作，阻抗圆图可以转换为导纳圆图，这对于处理不同类型的微波网络非常有用。 Smith圆图的应用主要包括以下几个方面： 1. 寻找r=1的等电阻圆和x=1的等电抗圆的交点，这可以帮助确定理想的匹配阻抗。 2. 读出反射系数Γ的幅度和相位，这对于计算和调整网络参数至关重要。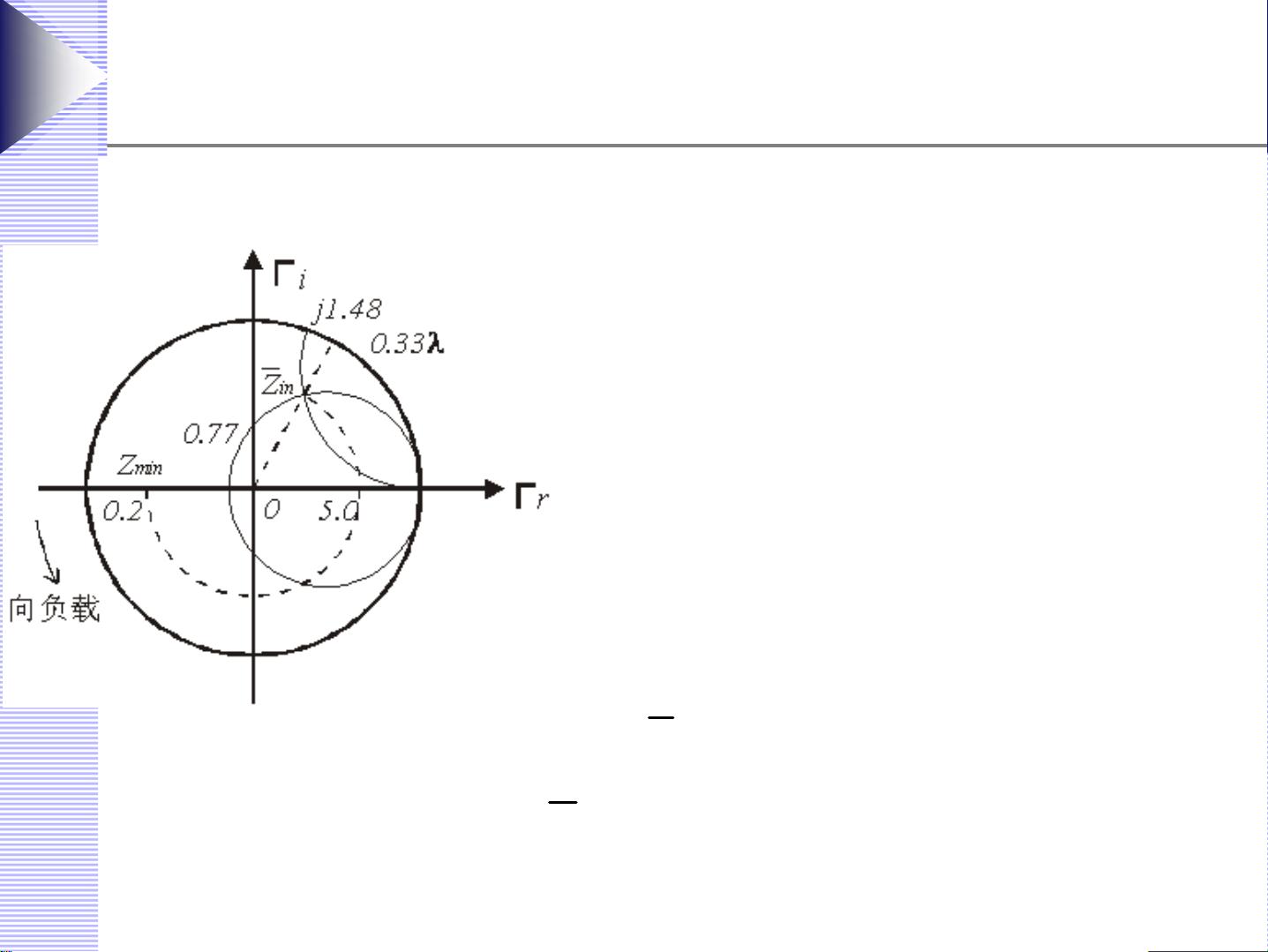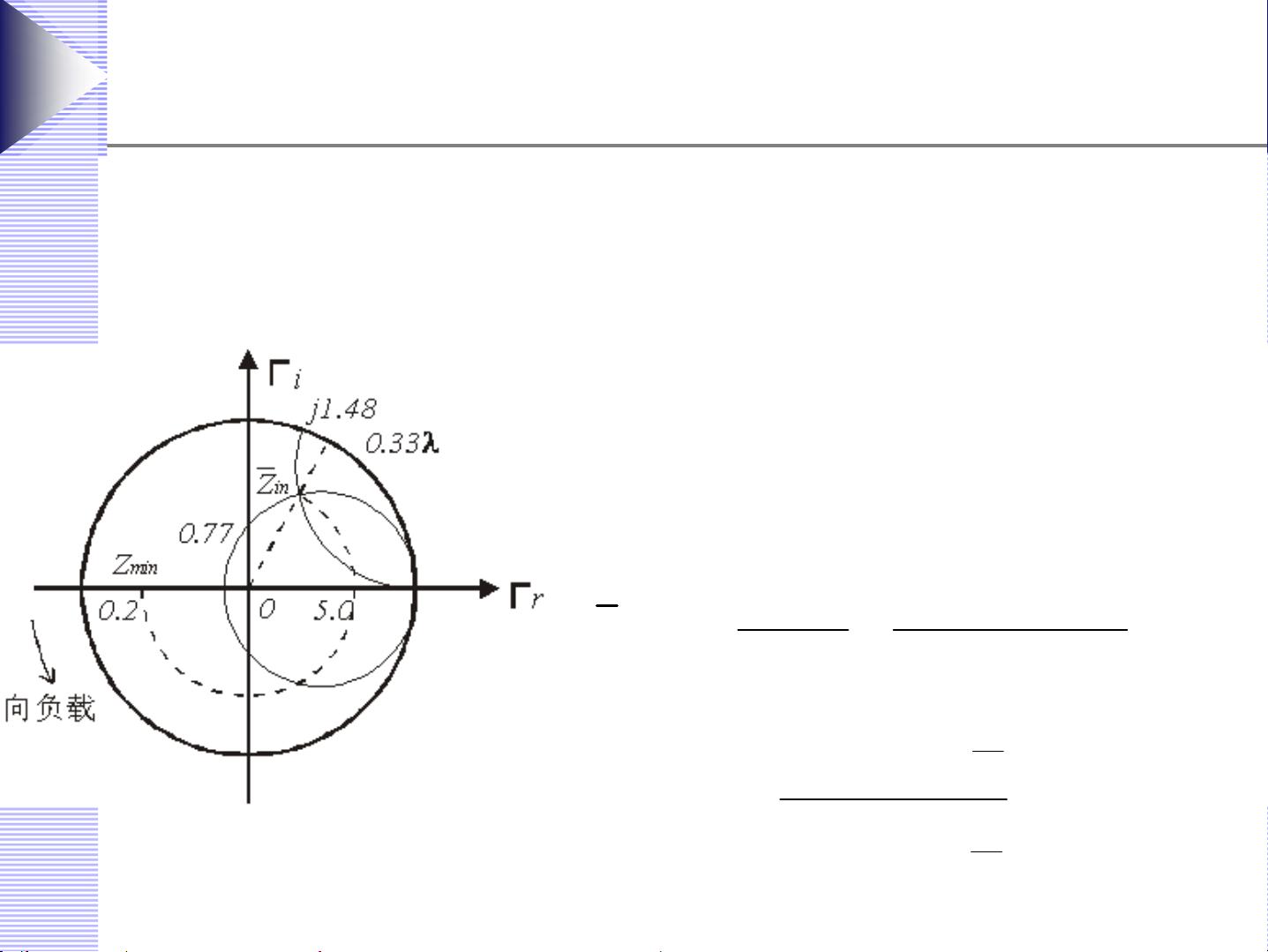 3. 找到Γ的等反射系数圆与正实轴的交点，即电压波腹点，从而得到电压驻波比ρ，这是衡量系统匹配好坏的重要指标。 4. 通过反归一化过程，可以将圆图上的数据转换回实际的阻抗或导纳值，用于实际电路设计。 例如，在给定的案例中，已知阻抗Z = 1 + j1，可以通过Smith圆图找到对应的反射系数Γ，然后进一步计算出电压驻波比ρ。同样，如果已知Zin = 100 + j50，也可以通过相同的方法求解反射系数和ρ，首先进行阻抗归一化，然后在Smith圆图上进行操作。 Smith圆图是微波工程中不可或缺的工具，它简化了微波网络分析的过程，使得设计者能够更高效地进行阻抗匹配和系统优化。通过熟练掌握Smith圆图的使用，工程师们能够更好地理解和解决微波系统中的各种问题。