非单调分段线性忆阻神经网络的平衡点共存与局部μ稳定性研究

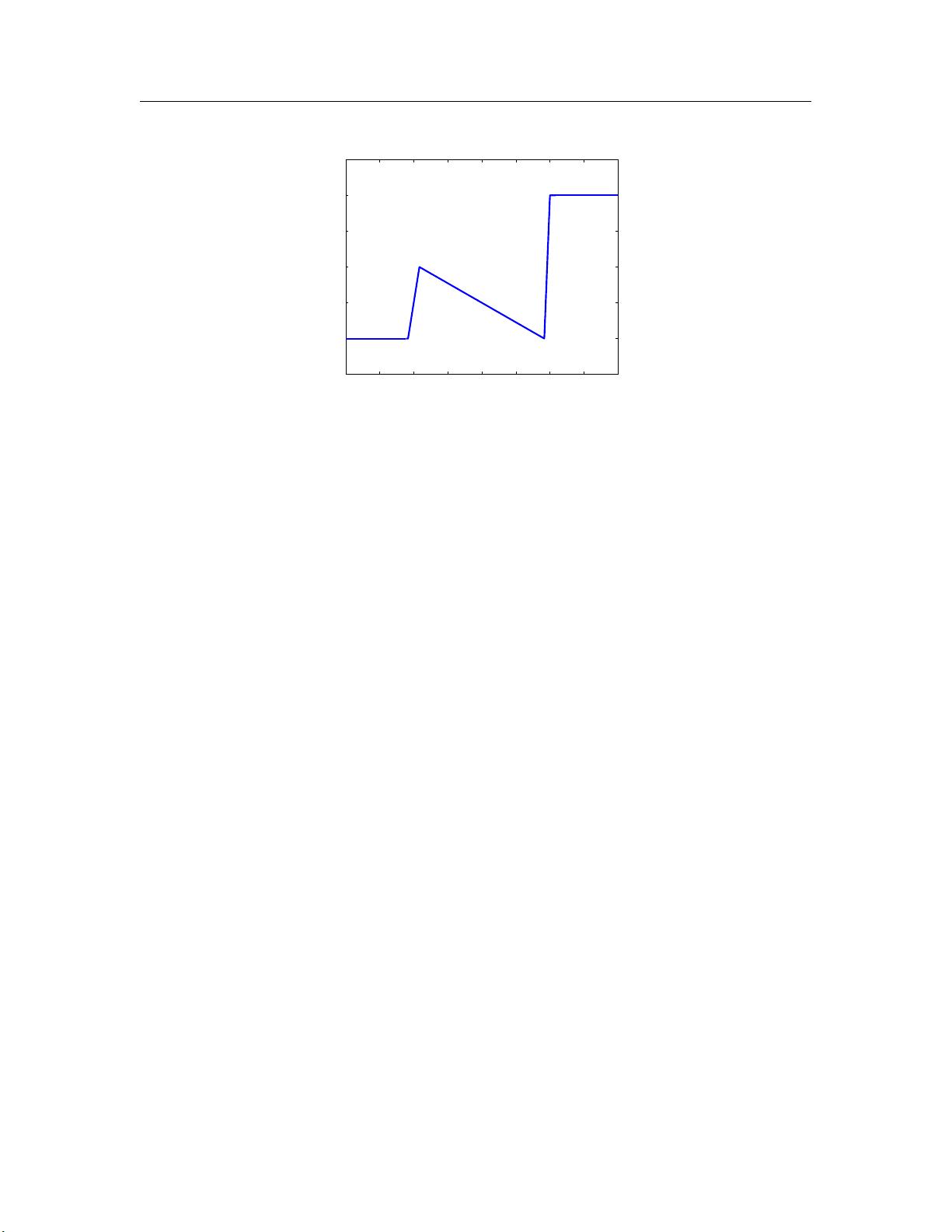
本文主要探讨了带有非单调分段线性激活函数和无界时变时滞的忆阻神经网络（Memristive Neural Networks, MNNs）的复杂动力学特性。忆阻器是一种新型的非线性电阻器，其电阻值不仅取决于电流强度，还取决于过去的历史电流，因此在神经系统和人工神经网络中有重要应用。研究的核心焦点在于这类MNN模型中的多个平衡点。 平衡点是指系统状态在没有外部输入时不会改变的状态。当神经网络具有非单调的分段线性激活函数时，这意味着激活函数在某些区间内可能表现出非单调性，这会导致系统的动态行为更加丰富和复杂。非单调性使得网络在不同输入下可能出现不同的响应，从而产生多个可能的稳定或不稳定的平衡状态。 作者聂小兵、郑卫星和曹进德通过不动点定理和非光滑分析理论进行深入研究，证明了对于n个神经元的网络，可以存在多达5n个平衡点，其中令人关注的是，这些平衡点中有3n个被证明是局部μ-稳定的。μ-稳定性是一种介于全局稳定性和局部稳定性的中间状态，它保证了即使在小的扰动下，系统也会返回到邻近的平衡状态，但并非所有方向上都稳定。 这个发现对于理解和控制这类忆阻神经网络至关重要，因为它揭示了系统的潜在动态结构。通过局部μ-稳定性，可以设计出有效的控制器来确保网络在实际应用中的稳定性能，如在控制系统、信号处理或机器学习中的应用。此外，文中还提供了多指数稳定、多幂率稳定和多对数稳定的判据，这些判据可以直接用于指导实际系统的设计和分析，确保其性能满足特定的稳定性和收敛速度要求。 这篇首发论文深入探讨了非单调分段线性激活函数和无界时滞条件下忆阻神经网络的多重平衡点性质及其稳定性，为理解这类复杂系统的行为提供了理论基础，并为实际应用中的控制策略设计提供了有价值的方法和准则。