The rest of the paper is organized as follows: In Section 2,
we describe the roles of the PSPs and the SSP in the
spectrum trading and define the reward function for the
SUs as well as the risk function for OSA. We introduce
related concepts to band-mix selection including band-mix
selection rule, efficient OSA curves and the SSP’s utility
function in Section 3. We elaborate on the two proposed
risk metrics for OSA: the X loss and the expected X loss in
Section 4. With the discritized version of the expected X
loss, we illustrate the optimal band-mix selection of the SSP
for OSA in Section 5. Finally, we cond uct numerical
simulations and analyze the performance results in Sec-
tion 6, and draw the concluding remarks in Section 7.
2SYSTEM MODEL
2.1 Spectrum Market
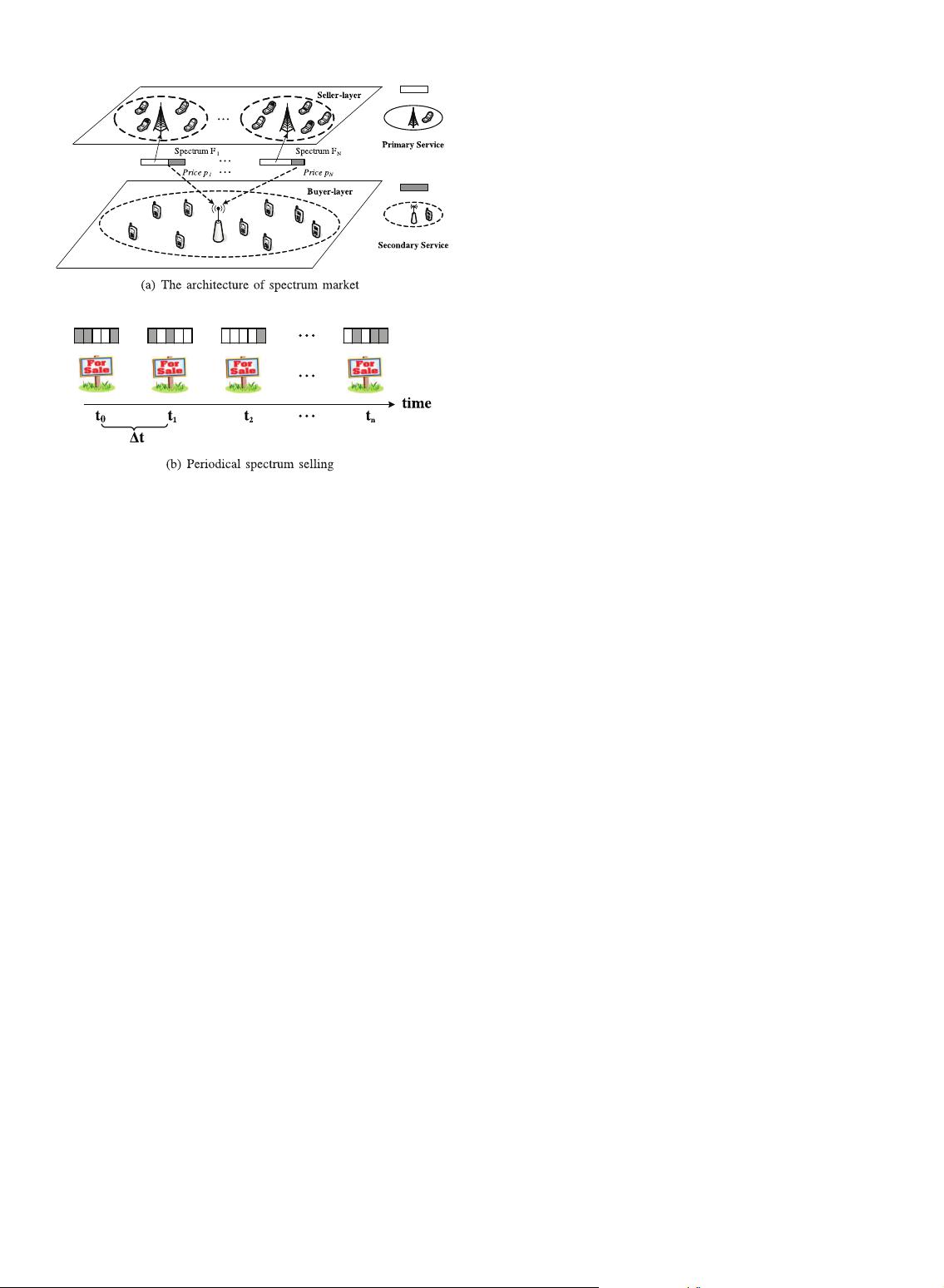
We consider a spectrum market in cognitive radio networks
[16] with multiple PSPs operating on different spectrum
bands and a SSP who serves a group of SUs as shown in
Fig. 1a. The SUs can take opportunistic use of these licensed
spectrum bands when the primary services are not on, but
must evacuate from these bands immediately when
primary services become active. In addition, we assume
all the spectrum transactions take place at starting time of
each period
3
as shown in Fig. 1b, and the payment for
spectrum trading is nonrefundable.
In this case, PSPs will set reasonable prices for the
unoccupied bands considering the quality of the bands as
well as competition among the PSPs in the spectrum market
[13], [15], [16], and sell those bands periodically for
monetary gains. Correspondingly, if the SSP (e.g., the base
station (BS) or the access point (AP)) realizes there is not
enough radio resource for the traffic demands of its SUs,
the SSP will play the role of trading agent for the SUs [6].
Specifically, the SSP will try to select a mix of currently
vacant licensed bands, buy those bands from the PSPs,
charge the SUs with the prices set by PSPs and share the
bands purchased among multiple SUs in a time-division
multiple access (TDMA) manner.
2.2 SSP’s Revenue and Risk Function
Assume there are n available spectrum bands owned by
different PSPs with identical bandwidth, which is equal to
1, within the sensing range of the SSP. Considering the
unpredictable activities of primary services, the uncertain
spectrum supply of different bands for a given period is
represented by ss ¼ðs
1
;s
2
; ...;s
n
Þ, where s
i
is a random
variable
4
within the domain of ½0; 1. Suppose, the total
traffic demand from the SUs is 1, and the proportional
composition of the band-mix that the SSP picks up is
!! ¼ð!
1
;!
2
; ...;!
n
Þ, !! 2W, where
P
n
i¼1
!
i
¼ 1. Then, the
total spectrum resources the SSP can obtain is
P
n
i¼1
s
i
!
i
,
and the expected reward for the SSP can be written as
ð!!Þ¼r
X
n
i¼1
IE ½s
i
!
i
; ð1Þ
where r is a constant, representing the SSP’s reward for
satisfying one unit of traffic.
5
Correspondingly, the risk
function of the SSP can be expressed as
‘ð!!; ssÞ¼pp
T
!! rss
T
!!; ð2Þ
where pp ¼ðp
1
;p
2
; ...;p
n
Þ is the charging price vector set by
the PSPs for OSA per period, and p
i
is a constant during a
spectrum trading period. Note that p
i
p
j
,ifIE ðs
i
ÞIE ðs
j
Þ.
Since r is a fixed number and ss is a random vector, the risk
for OSA depends on both the statistical characteristics of ss
and the SSP’s selection of bands belonging to the PSPs.
3PRIMARY CONCEPTS FOR BAND-M IX SELECTION
3.1 Band-Mix Selection Principle
Intuitively, the SSP is able to maximize his revenue by
pouring all the traffic of SUs over a particular band with the
maximal expected reward. However, the risk of using that
band may be quite high. A rational or risk-averse SSP is not
likely to gamble all the traffic on one band since the reward
may be extraordinarily low considering the activities of
primary services.
Therefore, the expected reward should not be the only
criterion in choosing the spectrum bands to access; instead,
the risk of the reward must be considered by the SSP. It is
reasonable to believe that if any two band-mixes have the
same expected reward, the SSP will prefer the one having
the smaller risk for OSA, and if any two band-mixes have
the same risk, the SSP will prefer the one having the greater
expected reward. So, the criterion for band-mix selection is
as the follows.
PAN ET AL.: THE X LOSS: BAND-MIX SELECTION FOR OPPORTUNISTIC SPECTRUM ACCESSING WITH UNCERTAIN SPECTRUM SUPPLY... 2135
Fig. 1. System model for spectrum trading.
3. The selling/buying period 4t should not be too long (e.g., days,
months, or years) to make dynamic spectrum access infeasible, and it
should not be too short (e.g., milliseconds or seconds) to incur over-
whelming overhead in spectrum trading. The typical duration is minutes or
hours as shown in [32]. In the rest of paper, we assume that all the spectrum
transactions are of fixed duration, so that the time parameter is not included
in our formulation.
4. Here, s
i
can be interpreted as unoccupie d time or unoccupied
bandwidth by primary services for band i during one time period.
5. With the assumption that r is fixed, ð!!Þ can also be interpreted as the
expected traffic demands that the SSP is able to support.









