MATLAB牛顿迭代法课程设计详解

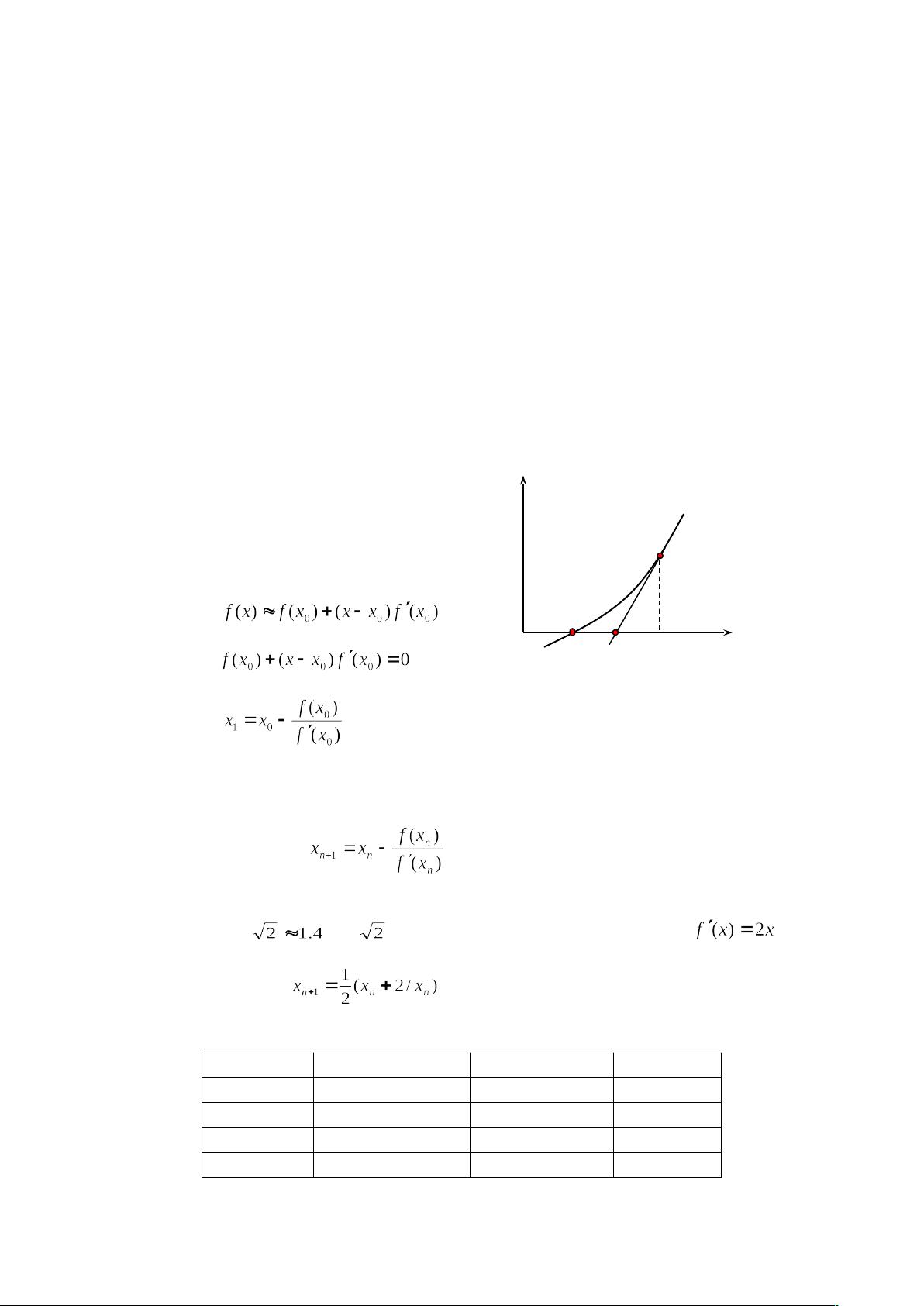
“matlab牛顿迭代法的课程设计实验指导，适合机器学习的同学。” 这篇文档是关于使用MATLAB进行牛顿迭代法的课程设计实验指导，主要针对的是机器学习领域的学生。牛顿迭代法是一种在数值分析中解决非线性方程的高效方法，它基于微积分中的局部线性化思想。这种方法由牛顿提出，适用于求解单个非线性方程或非线性方程组的数值解。 牛顿迭代法的核心在于通过初始猜测值x0，利用函数f(x)在x0处的切线来近似原函数，并解这个切线与x轴的交点，作为下一次迭代的近似解。迭代公式可表示为： \[ x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} \] 这里的\( f(x_n) \)是函数在点x_n的值，\( f'(x_n) \)是函数在该点的导数值。每次迭代都会使得新的解x_{n+1}更接近真实解x*，因为切线比函数本身更平缓，所以迭代速度较快。 牛顿迭代法的收敛速度是其主要优点，它具有二阶收敛性质。这意味着每次迭代后，解的误差平方会减半，对于求解高精度的数值问题非常有效。例如，在平方根的计算中，通过牛顿迭代法可以快速得到精确结果。 在实际应用中，比如在机器学习中，我们可能需要求解复杂的优化问题，牛顿法可以用来找到目标函数的局部极小值。然而，牛顿法也有其局限性，例如要求函数的导数存在且可计算，对于一些复杂或非光滑的函数可能不适用。此外，如果初始猜测值远离真实解，迭代可能会发散，或者收敛速度会变得很慢。 在MATLAB中实现牛顿迭代法，通常涉及到以下几个步骤： 1. 定义目标函数f(x)和它的导数f'(x)。 2. 选择一个初始值x0。 3. 计算f(x0)和f'(x0)。 4. 应用迭代公式更新x值。 5. 检查收敛条件，如连续两次迭代的差异小于某个阈值，或者达到最大迭代次数。 6. 如果未达到收敛条件，返回步骤3。 在给出的实验示例中，求解方程\( f(x) = x^2 - 2 = 0 \)的根，可以使用牛顿迭代公式\( x_{n+1} = x_n - \frac{x_n^2 - 2}{2x_n} \)。初始值取为1.4，经过几次迭代后，解的精度迅速提高，误差显著减少。 牛顿迭代法是MATLAB中解决非线性问题的一个强大工具，尤其在机器学习中，优化问题的求解经常需要用到这种高效的方法。通过理解并熟练掌握牛顿迭代法，可以提升解决实际问题的能力。