清华大学数据结构-图课件详解

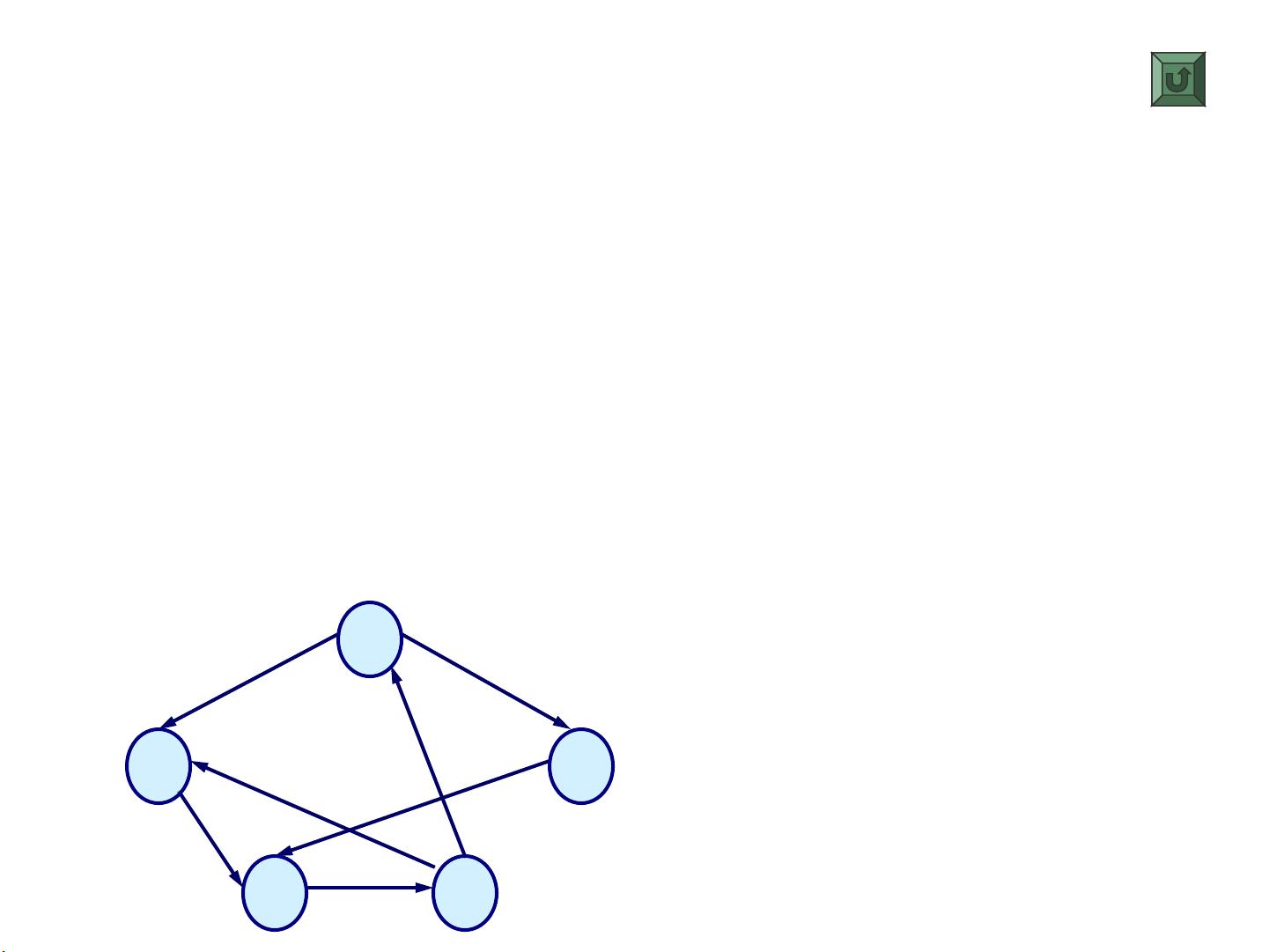
"这是一份来自清华大学的关于数据结构中图的课程课件，由严蔚敏教授讲解。课件详细介绍了图的抽象数据类型、存储表示、遍历方法、最小生成树、最短路径问题、拓扑排序以及关键路径等核心概念。" 在计算机科学中，数据结构是组织和管理数据的重要方式，而图是一种复杂的数据结构，用于表示对象间的关系。图由一个顶点集V和一个弧集R构成，记作Graph=(V,R)，其中R包含所有从顶点v到顶点w的弧，<v,w>表示从v到w的有向边，v是弧尾，w是弧头，且通常附带有定义边意义的谓词P(v,w)。 图的类型可以分为有向图和无向图。有向图中，弧是有方向的，如G1=(V1,VR1)，包含多个有向边如<A,B>、<A,E>等。无向图则由顶点集和边集构成，没有方向，如G2=(V2,VR2)，其中{(A,B)}表示A和B之间有一条边，而不区分方向。 图的相关术语包括但不限于： 1. 子图：如果图G'=(V',VR')的顶点集V'和边集VR'都是原图G=(V,VR)的一部分，那么G'是G的子图。 2. 网、子图、完全图、稀疏图和稠密图：网是有权重的图，完全图是任意两个顶点间都有边的图，边数为n(n-1)/2（无向）或n(n-1)（有向）。稀疏图和稠密图是根据边的数量相对于顶点数量来区分的，边数小于nlogn的图被认为是稀疏图，反之则为稠密图。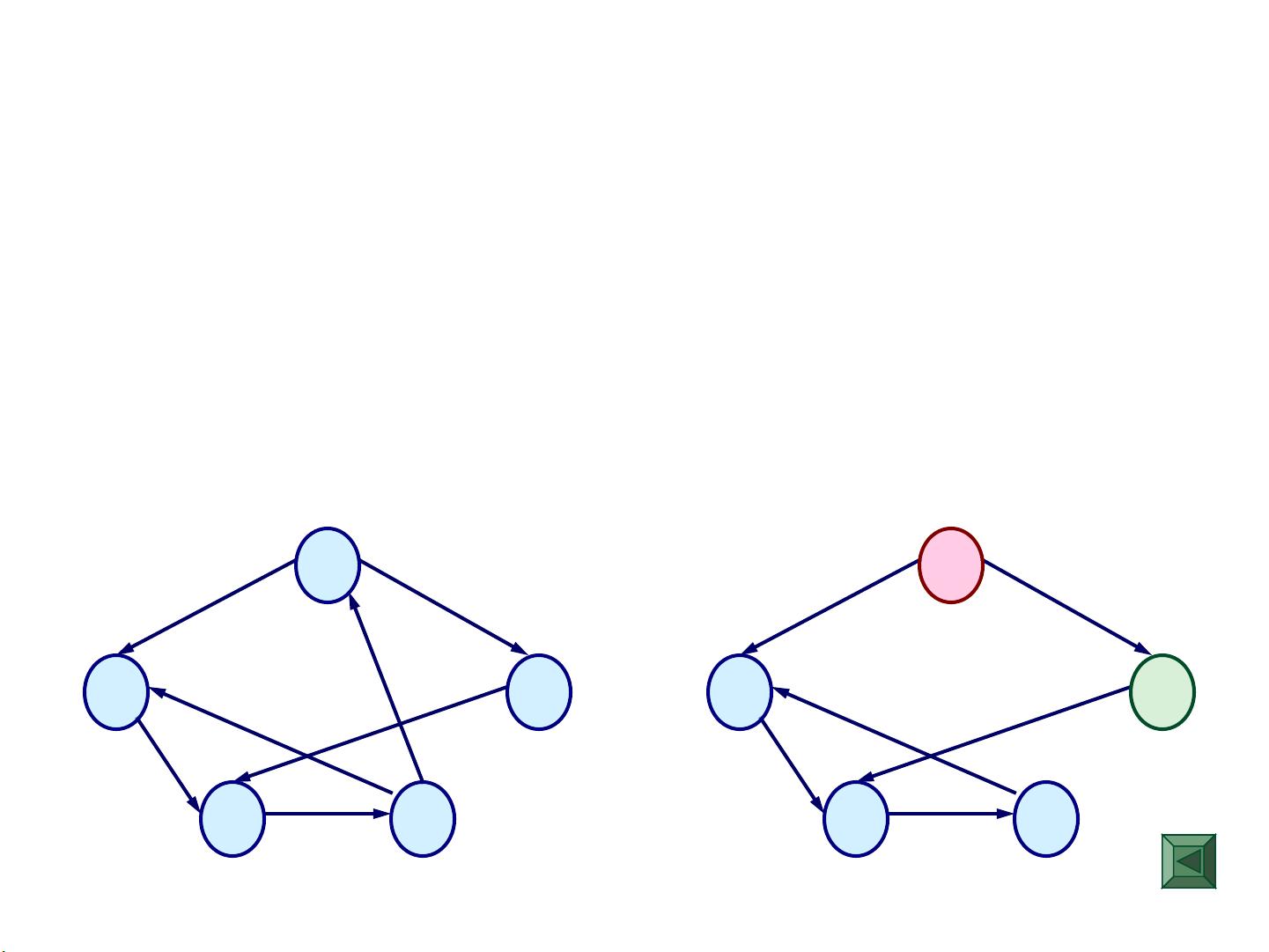 3. 邻接点、度、入度和出度：邻接点指的是通过边相连的顶点；度是与顶点相关的边的总数，包括出度（以顶点为起点的边数）和入度（以顶点为终点的边数）。 图的遍历是图论中的基础操作，包括深度优先搜索(DFS)和广度优先搜索(BFS)，用于访问图中所有的顶点。最小生成树算法，如Prim's和Kruskal's算法，用于找到连接所有顶点的权值最小的边集合。最短路径问题，如Dijkstra算法和Floyd-Warshall算法，用于找出两点间最短路径。拓扑排序用于有向无环图(DAG)，给出一个线性的顶点顺序。关键路径则是项目管理中的概念，用于找出决定项目最早完成时间的关键任务序列。 这份课件详细阐述了这些概念，对于理解和应用图的理论知识非常有帮助，特别适合计算机科学的学生和从业者进行学习和参考。