C语言实现的PID算法教程：原理与示例

PID算法是一种广泛应用在工业自动化领域的控制策略，由比例(P)、积分(I)和微分(D)三个部分组成，旨在通过线性组合优化控制系统的响应和稳定性。本文档详细介绍了如何在C语言中实现增量式PID算法，针对51单片机平台设计。 首先，PID控制器的基本原理是根据输入偏差(e(t))计算控制量(u(t))，公式如下： \[ u(t) = K_p \cdot e(t) + K_i \cdot \int_{0}^{t} e(\tau)d\tau + K_d \cdot \frac{de(t)}{dt} \] 其中，\( K_p \)、\( K_i \)和\( K_d \)分别代表比例、积分和微分增益。 1. **比例控制** (P): 只考虑当前的偏差，快速纠正误差，但无法消除稳态误差。如果增益过大，可能导致系统不稳定。 2. **积分控制** (I): 通过累加误差的时间积分来减小稳态误差，但单独使用积分可能会导致调节动作过慢，系统响应延迟。 3. **微分控制** (D): 基于误差的变化率，能够预测未来误差趋势，加快系统响应，尤其在滞后系统中有显著效果，但对噪声敏感。 在实际应用中，如单回路控制系统中，PID控制器根据控制需求灵活选择组合形式，如比例控制(P)，比例积分(PI)，或比例积分微分(PID)。比例+积分(PI)控制器可以确保系统在稳态下没有稳态误差，而比例+积分+微分(PID)则提供了更全面的动态性能和快速响应能力。 该C语言程序提供了一种实现PID算法的基础框架，适用于51单片机这样的嵌入式设备，适合用于温度、压力、流量等工艺参数的自动控制。理解并掌握PID算法的关键在于正确调整各增益参数，同时处理好控制系统的动态响应与稳定性的平衡。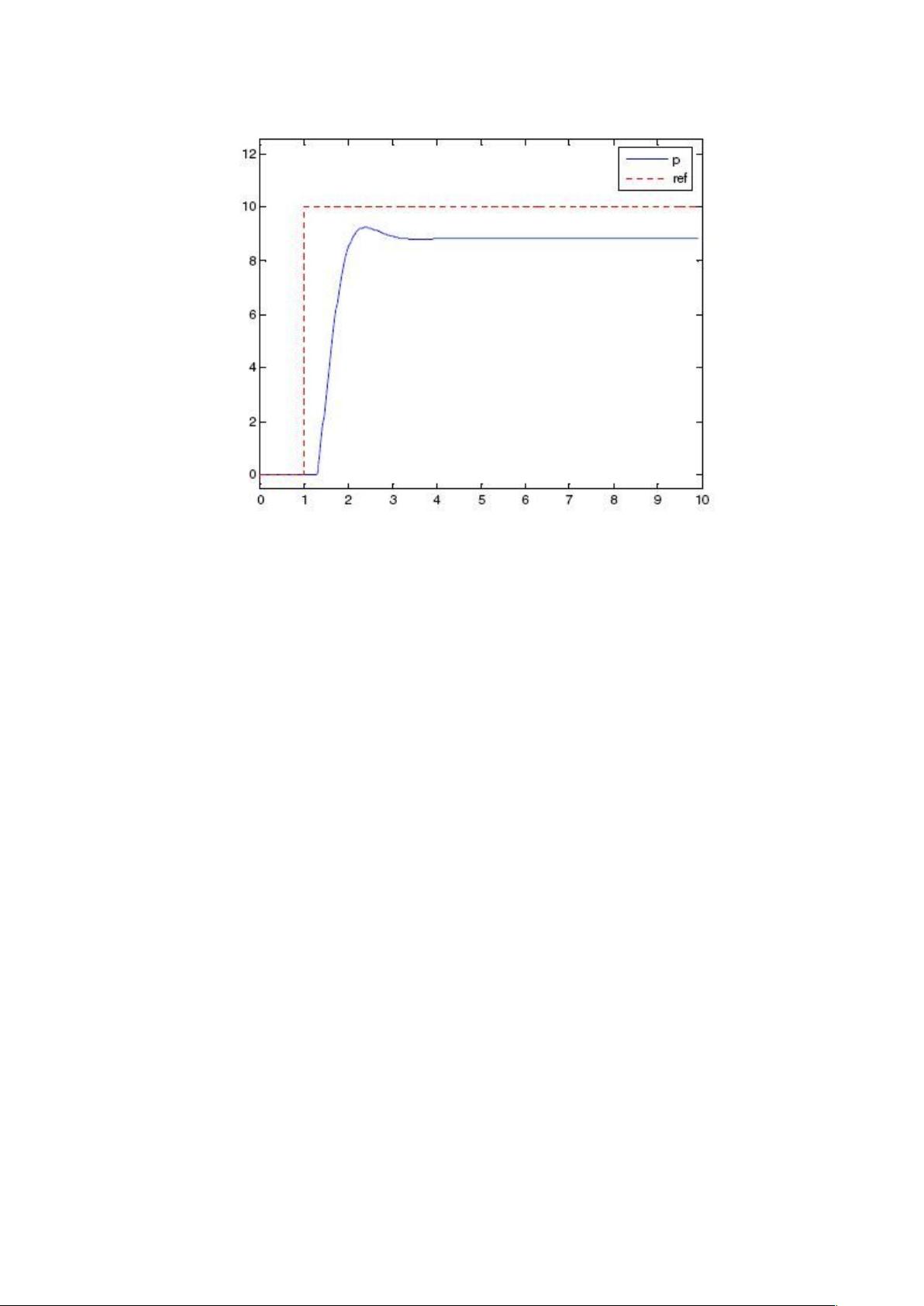 此外，文档还提到了控制器的阶跃响应图，展示了不同控制策略下的系统响应特性，这对于理解和调试PID控制器的性能至关重要。理解这些原理和图形可以帮助工程师更好地设计和优化PID算法以适应具体的应用场景，提高系统的控制精度和效率。