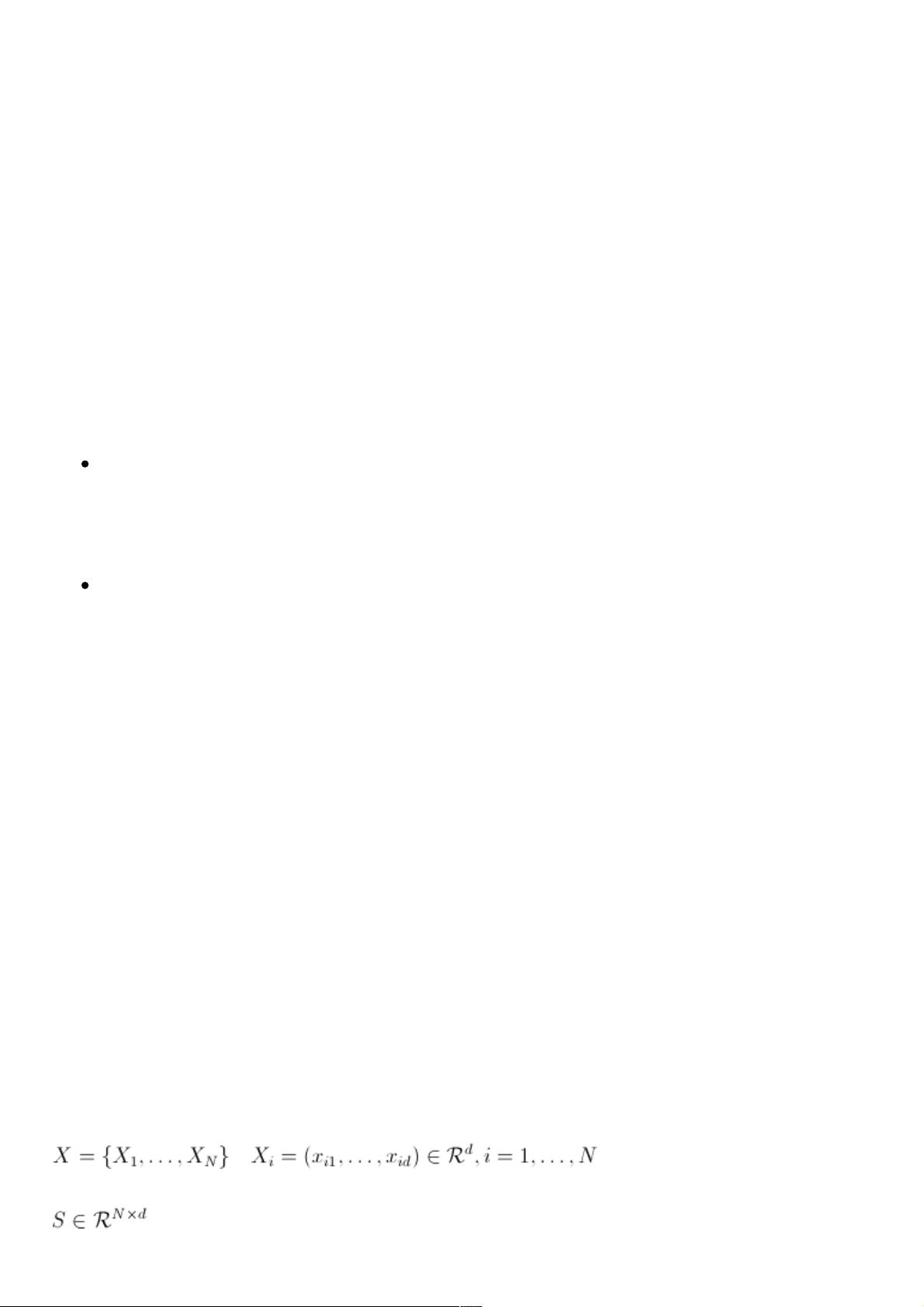PCA降维原理与应用：主成分分析深度解析

PCA（主成分分析）是一种强大的统计方法，最初在19世纪末至20世纪初由研究者提出，主要用于高维数据的降维和特征提取。它在众多领域，如机器学习、数据分析和信号处理中发挥着核心作用，特别适合于减少复杂数据集中的噪声和冗余维度。 PCA的核心概念是基于数据的协方差矩阵。协方差矩阵反映了各个变量之间的线性关系，其特征值和特征向量对于理解数据的结构至关重要。当处理大量变量且变量间存在相关性时，协方差矩阵可以帮助我们找到数据的主要方向或模式。通过计算协方差矩阵的特征分解，我们可以得到一组按重要性排序的主成分，每个主成分都是原始变量的线性组合，但消除了噪声和冗余信息。 在PCA的具体应用中，我们首先要计算样本数据的中心化版本，即将每个变量减去其均值，使得协方差矩阵反映的是变量间的实际差异而非平均值。接着，我们求解协方差矩阵的特征值问题，得到一组对角化的矩阵，其中最大的特征值对应于第一个主成分，依次类推，后续的主成分代表了剩余变异性的最大方向。 降噪的过程体现在选择具有较大特征值的主成分，这些主成分与原始数据的方差紧密相关，而噪声导致的干扰往往表现为较小的特征值。通过保留这些重要的主成分，我们可以在保持数据主要信息的同时，剔除掉噪声带来的影响。冗余维度则表现为特征值接近于零的主成分，它们对数据的区分能力弱，因此在降维过程中会被剔除。 举例来说，如果我们在图像处理中遇到一个包含大量像素的图片，PCA可以帮助我们找到图像中最关键的颜色或纹理特征，而不是无意义的像素细节。或者在金融数据中，PCA可以帮助识别影响市场波动的主要因素，去除无关的随机波动。 PCA是数据预处理的重要工具，它通过优化数据的投影方式，使得降维过程既保持了数据的本质特征，又有效地减少了复杂性和噪声的影响。理解并熟练运用PCA，能够极大地提升在实际问题中的数据分析效率和模型构建效果。