MATLAB实现的蒙特卡洛模拟在热传递中的应用

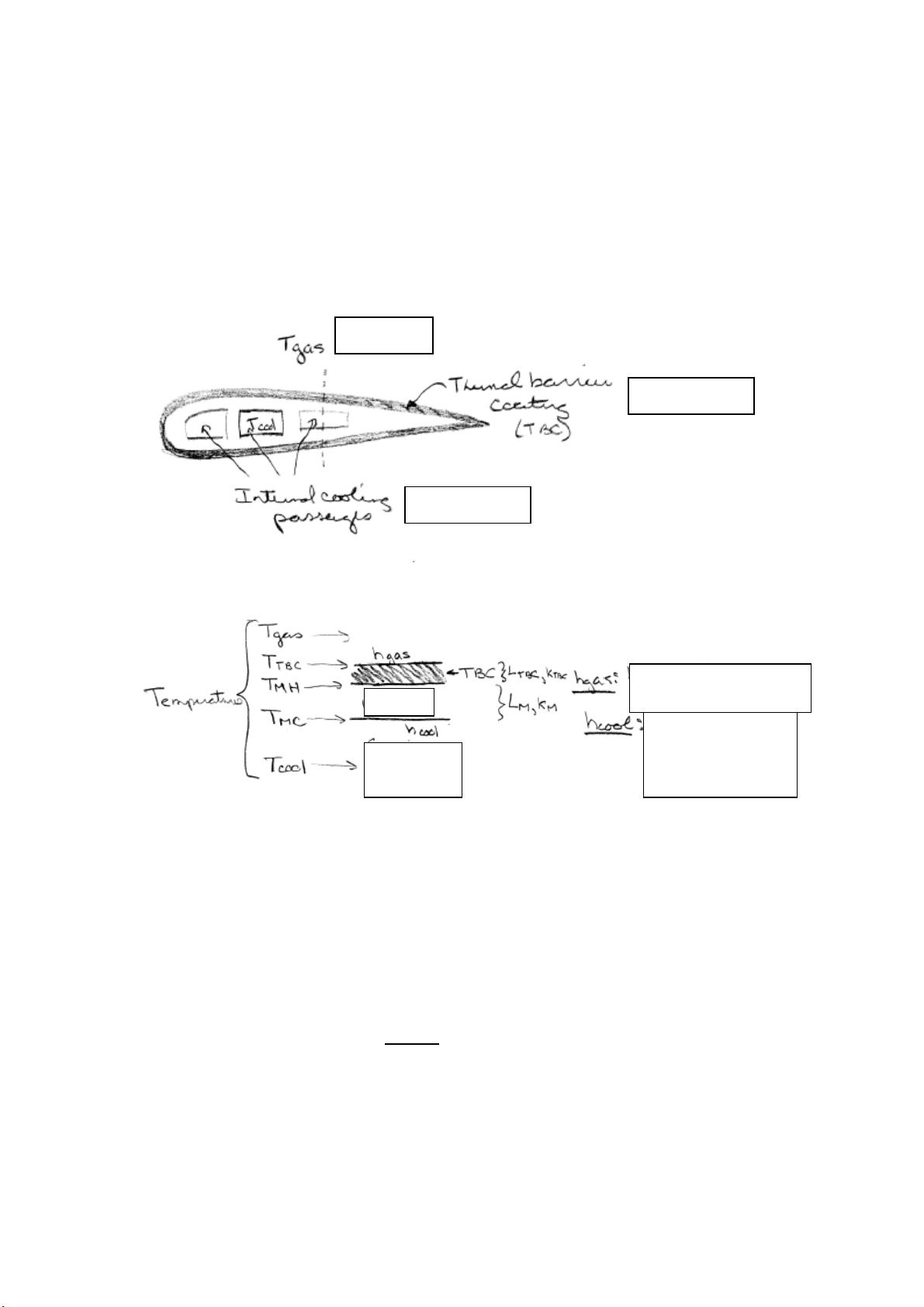
"通过一个冷涡轮叶片的热传递模型，使用MATLAB实现蒙特卡洛模拟，探讨一维热传导方程及应用" 在热力学和工程领域，蒙特卡罗模拟是一种强大的数值计算方法，它利用随机抽样或统计试验来解决复杂问题。在本例中，该方法被用于验证一个简化版的热传递模型，涉及到通过涡轮叶片的冷气流。涡轮叶片的横截面包括气体通道、涂层以及内部冷却通道，这些因素共同影响着热量的传递。 热传导模型通常基于傅里叶定律，该定律描述了热量如何在不同材料之间传递。在本问题中，我们有一维热传导模型，它由两个关键的热传递系数表示：气体中的热传递系数（gas h）和冷却通道中的热传递系数（cool h），以及两个材料的热导率（k，分别对应金属叶片和TBC涂层）。模型的目标是解决四个未知量：金属热边的温度（TBC T）、金属冷边的温度（MM T和MC T）以及冷却流体的热流密度（q）。 为了解决这些未知量，我们建立了一个线性方程组，其中包含了气体温度、气体热传递系数、材料热导率、长度和热流密度等参数。方程组的解给出了各个变量的具体值，有助于分析叶片的温度分布和热流情况。在实际模拟中，我们使用了特定的初始参数，例如气体温度、热传递系数和材料特性，以此计算出最终的温度分布和热流密度。 在模拟结果中，金属热边温度（MH T）为835℃，金属冷边温度（TBC T）为1114℃，而涂层侧温度（MC T）为758℃，冷却流体的热流密度（q）为5.5810 W/m²。这些数值对于评估叶片的热状态和预测其寿命至关重要。较高的温度可能导致材料疲劳，从而缩短叶片的使用寿命，因此降低MH T是优化设计的关键目标。 在工业实践中，由于生产过程中的不确定性，材料属性可能会有一定的变化。例如，热传递系数和热导率可能存在一定的随机波动，这可以通过引入参数的均匀分布不确定性来考虑。通过蒙特卡洛模拟，我们可以对这些不确定性的影响进行量化，从而得到一系列可能的结果，帮助工程师评估设计的鲁棒性和优化方向。 总结来说，这个MATLAB实现的蒙特卡洛模拟例子展示了如何运用随机抽样技术解决复杂的热传递问题，特别是在涡轮叶片这样的高精度工程组件中。通过模拟，我们可以理解不同参数变化如何影响叶片的热性能，并为优化设计提供数据支持。