贝叶斯网络与信息理论
需积分: 16 89 浏览量
更新于2024-07-18
收藏 3.82MB PPT 举报
"该资源主要涉及的是贝叶斯网络及其相关知识,包括对偶问题、图理论、K近邻算法、相对熵与互信息、信息增益等概念。"
贝叶斯网络是一种概率图模型,它利用贝叶斯定理来表示变量之间的条件概率关系。在贝叶斯网络中,节点代表随机变量,边则表示变量之间的依赖关系。这种网络结构允许我们进行概率推理,即根据已知证据推断未知事件的概率。在大数据和人工智能领域,贝叶斯网络常用于决策支持、预测分析和不确定性管理。
对偶问题在数学优化中是一个重要的概念,通常与原问题相对应,特别是在线性规划中。这里的例子提到的是一个组合优化问题,寻找一组整数使得它们的和等于特定值s,这可以通过动态规划或贪心策略来解决。
Delaunay三角剖分是一种几何图形分割方式,它保证没有一个点位于其相邻三角形的内部,形成了Voronoi图的对偶图。这种剖分在计算机图形学、地理信息系统和网络设计中有广泛应用。
K近邻图(K-Nearest Neighbor Graph, K-NN图)是数据挖掘中的一个概念,其中每个节点连接其最近的K个邻居。K-NN图的性质指出,节点的度至少为K,而在K互近邻图中,节点的度最多为K。这些图可以用于聚类、分类和其他数据探索任务。
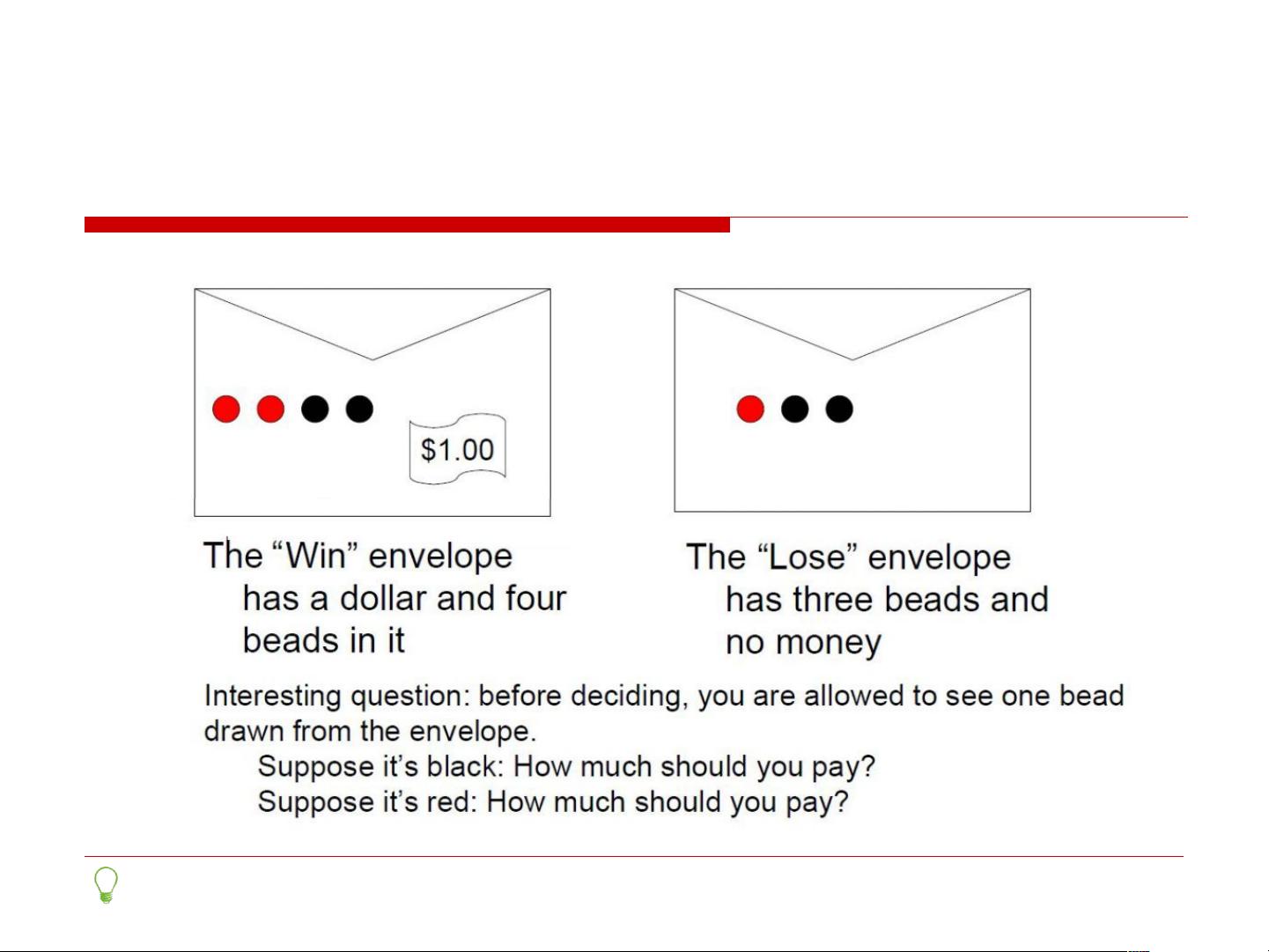
相对熵,又称互信息或Kullback-Leibler散度,是衡量两个概率分布p(x)和q(x)之间差异的度量。它不是对称的,即D(p||q)通常不等于D(q||p),且总是非负的。相对熵在信息论和机器学习中用于评估模型的复杂性和拟合度,例如在变分推理中,通过最小化KL散度来逼近复杂的后验分布。
互信息I(X,Y)是衡量随机变量X和Y之间依赖程度的量,它是联合分布与独立分布乘积的相对熵。互信息为正,当X和Y有关联;为零时,X和Y独立。
信息增益是决策树算法(如ID3、C4.5和CART)中用于选择最佳特征的重要指标,它衡量了特征A引入的额外信息,有助于减少类X的不确定性。
该资源涵盖了贝叶斯网络的基础、图论概念以及信息理论的关键点,对于理解和应用这些领域的知识非常有帮助。
2024-12-25 上传
2024-12-25 上传
2024-12-25 上传
2024-12-25 上传
weixin_43401371
- 粉丝: 0
- 资源: 2
最新资源
- Timepiece:台式机闹钟-开源
- celaju:达托斯基地
- dbt-learn-myang
- HT-Microservices:人类谈微服务
- Paddle2.0-API:高层API助你快速上手深度学习
- Salat-App:使用React Native创建的Salat Time应用
- esp_effects:ESP32的老派演示效果
- filecon9
- Activity_selection_prblm.c
- 针对Web开发人员HTML-CSS和Javascript:Coursera测试3
- Zobrollo:2D简约顶视图赛车游戏
- touchcreator.github.io
- Android-Activity:Activity之间传输数据
- stage-2assignments
- sReminder - Event and Birthday Reminder-开源
- 数据可视化平台-大屏.rar