模糊聚类分析原理与实现

"Matlab记录文本模糊聚类分析基本知识及实现023.docx" 模糊聚类分析是一种在数据分类中应用广泛的技术，特别是在处理数据不确定性或边界模糊的情况时。传统聚类分析如K-means或层次聚类，通常假设数据点完全属于某一个类别，但在实际问题中，数据点可能同时具有多个类别的特性，这就引入了模糊聚类的概念。 模糊聚类分析的基本思想是，通过计算样本与类别之间的相似度或关联程度，而不是简单的二元归属关系（即完全属于或不属于）。这允许样本同时属于多个类别，且对其所属类别的隶属度有一个连续的度量，从而更好地模拟现实世界中的复杂情况。 在模糊聚类中，模糊等价矩阵是一个关键概念。一个模糊相似矩阵R表示对象之间的相似程度，如果满足自反性（每个对象与自身相似），对称性（对象A与B的相似度等于B与A的相似度），以及传递性（如果A与B相似且B与C相似，那么A与C也相似），那么R就成为模糊等价矩阵。模糊等价矩阵可以看作是衡量对象之间关系的强度，而非简单的是/否判断。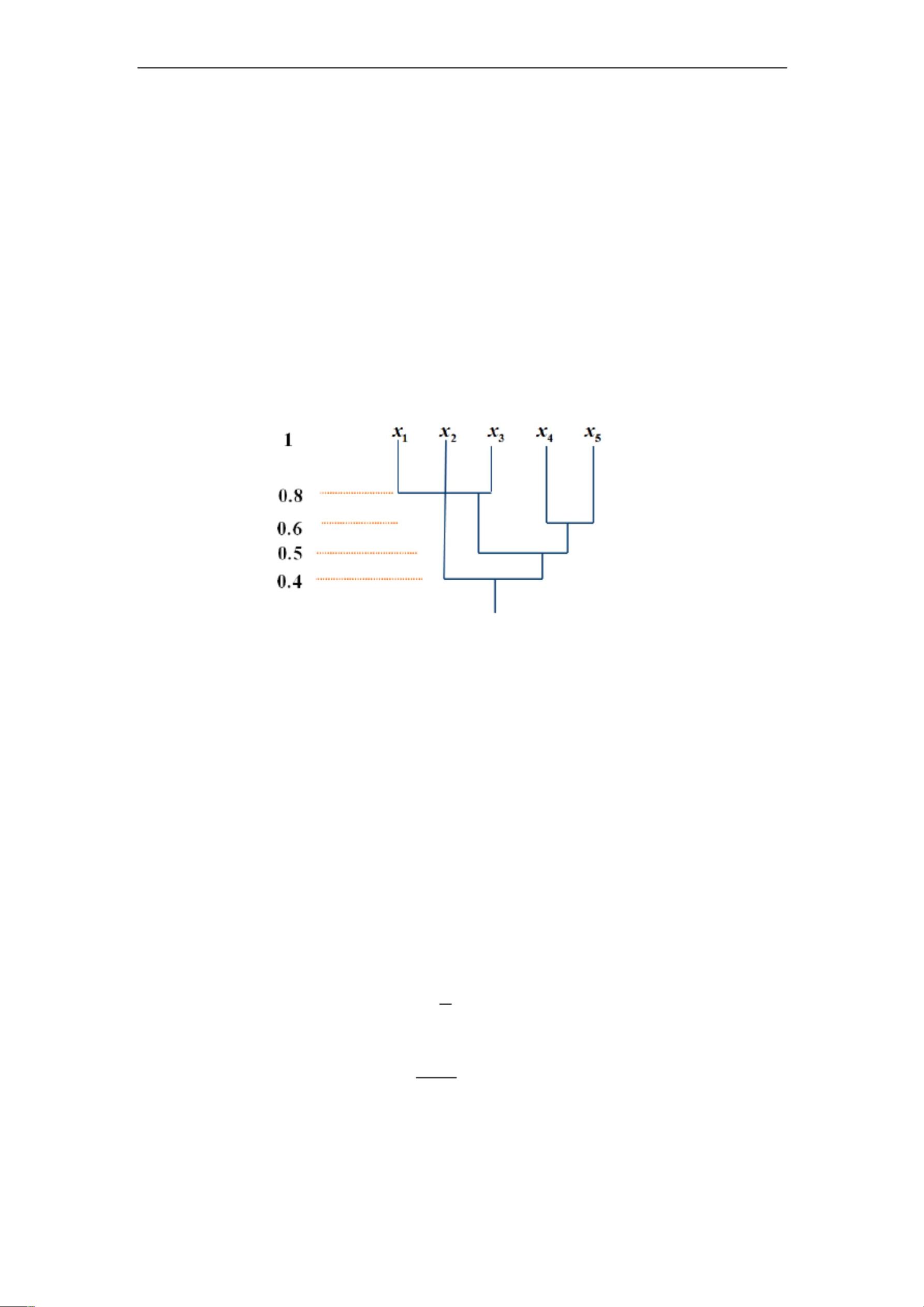 模糊等价矩阵的λ-截矩阵是模糊聚类的另一个核心工具。对于给定的模糊矩阵A和一个介于0到1之间的参数λ，λ-截矩阵A_λ将模糊矩阵转换为布尔矩阵，其中元素A_λ[i][j]为1当A[i][j] ≥ λ，否则为0。通过改变λ的值，我们可以得到一系列不同细化程度的分类，形成一个分类的分级结构，即聚类树。当λ增大，分类变得更细致；当λ减小，类别会合并，聚类结果变得更粗略。 举例来说，如果我们有5个对象U={1, 2, 3, 4, 5}，并给出一个模糊等价矩阵R，当λ=1时，所有对象之间的关系都被认为是最强的，即它们彼此都视为相似。随着λ减小，相似度阈值降低，分类可能会发生变化，某些对象可能会被归入同一个类别，因为它们在较低的相似度标准下仍然被认为足够相似。 在Matlab中，实现模糊聚类分析可以使用模糊逻辑工具箱（Fuzzy Logic Toolbox），该工具箱提供了如cmeans、fcluster等函数，用于执行模糊C均值聚类和基于模糊等价关系的聚类。用户可以调整聚类参数，如隶属度函数的形式、模糊因子等，以适应具体的数据和应用场景。 模糊聚类分析提供了一种更为灵活和精确的数据分类方法，尤其适用于那些数据边界模糊、类别重叠或存在不确定性的情景。在计算机科学尤其是数据分析和机器学习领域，模糊聚类分析有着广泛的应用，例如在图像分割、社交网络分析、客户细分等领域。通过深入理解和熟练运用模糊聚类，我们可以更好地理解和挖掘数据背后的模式和结构。