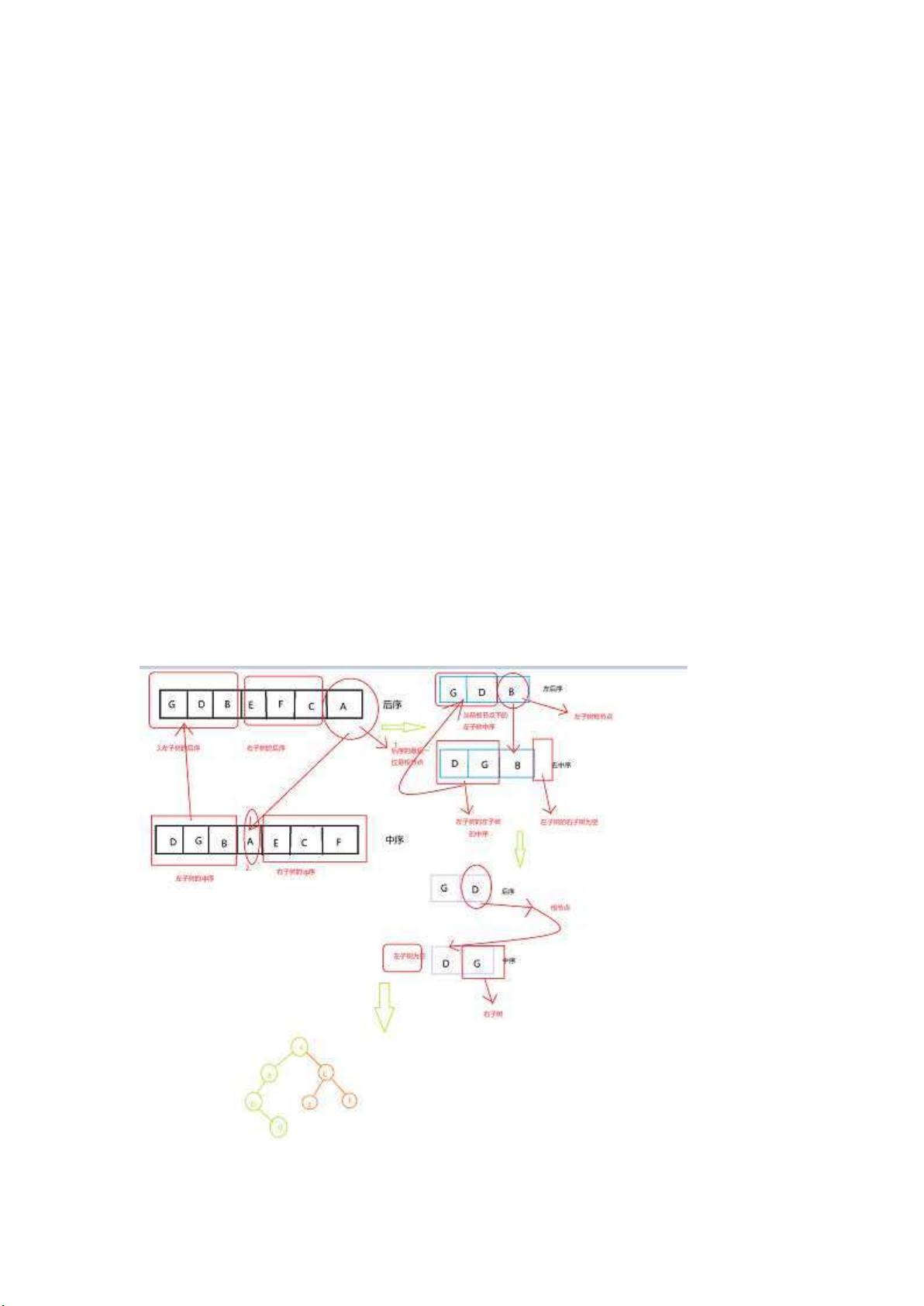
构建二叉树：根据后序与中序遍历

"这篇资源是关于如何利用后序和中序遍历序列来构建二叉树的程序实现，主要涉及数据结构中的二叉树概念，包括后序、中序遍历的特点以及递归和迭代的方法来创建二叉链表结构。" 在数据结构中，二叉树是一种重要的非线性数据结构，它由一个有限集合的节点组成，每个节点最多有两个子节点，通常分为左子节点和右子节点。二叉树的遍历有三种基本方式：前序遍历（根-左-右）、中序遍历（左-根-右）和后序遍历（左-右-根）。当给出二叉树的后序和中序遍历序列时，由于后序遍历的最后一个元素一定是根节点，而在中序遍历中，根节点将左子树和右子树分隔开，因此可以唯一确定这棵二叉树。 题目给出的后序遍历序列是"GBDFECA"，中序遍历序列是"DGBAECF"。根据这两个序列，我们可以手动构造出对应的二叉树。首先，后序遍历的最后一个元素"C"是根节点，在中序遍历序列中，"C"将序列分为了"DGBAE"和"F"两部分，分别对应左子树和右子树。接着，我们对左右子树重复这个过程，直至所有节点都确定。 在程序实现上，这个C语言代码定义了一个`BTNode`结构体，用于存储二叉树节点的数据元素、左孩子和右孩子。函数`creatBITree`接收后序遍历序列`pos`、中序遍历序列`in`和节点个数`n`作为参数，用于构建二叉树。它首先检查序列是否为空，然后初始化辅助数组来处理子树的遍历。在找到根节点之后，通过循环遍历中序序列来划分左子树和右子树，并递归地创建它们。 迭代方法的核心在于不断分割两个遍历序列，直到找到所有叶子节点。每次分割后，都会创建一个新的节点，设置其数据元素，并链接到已构建的子树。最终，当序列中只剩下一个元素或者没有元素时，递归返回，构建完整的二叉树。 在程序的最后，可以输出构建的二叉树的先序遍历序列，如题目所示的两种表示法：括号表示法和空格表示法。这两种方法都是为了直观地展示二叉树的结构。 总结来说，这篇资源提供了如何根据后序和中序遍历序列构建二叉树的思路和C语言实现，有助于理解二叉树遍历和构建的过程。对于学习数据结构和算法的人来说，这是一个很好的练习和参考资料。