Fisher线性判别法：降维与样本分类实践

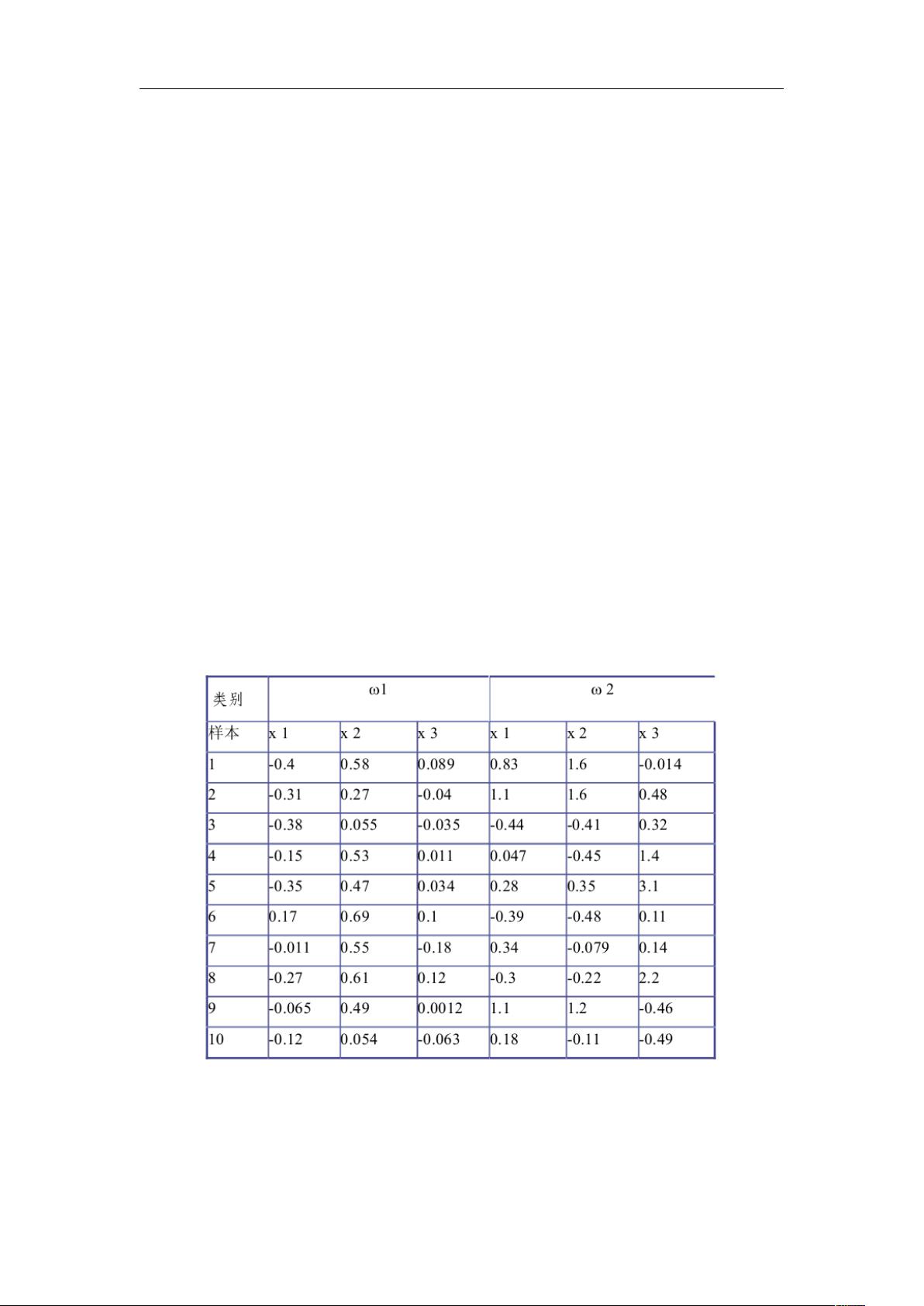
Fisher线性判别是一种统计学方法，用于解决高维数据的降维问题以及模式识别中的分类问题。它旨在找到最佳的投影方向，使得不同类别间的样本距离最大化，同时保持同一类别内的样本尽可能紧密聚类。这种方法特别适用于处理线性可分的数据集，当原始数据在高维空间中线性可分时，通过线性变换将其映射到低维空间，可以简化分类任务。 实验1的目标是让学生亲手实践Fisher线性判别算法，通过编写程序来理解其工作原理。首先，参与者需要改写一个通用函数，该函数接受三维数据并计算最优投影方向W，以确保在降维后仍能保持样本的线性可分性。接着，他们需要分析表1-1中的两个类别（ω1和ω2）数据，运用算法计算出这两个类别对应的最优投影方向，并在二维平面上绘制出投影后的数据点和最优直线。 在实际操作中，学生需要决定决策边界，例如，给定新的样本点xx1和xx2，通过已求得的方向W判断它们应归属哪个类别。这是一个应用Fisher判别理论的实际例子，通过新样本的投影位置来检验理论的有效性。 进一步地，如果时间允许，学生可以选择挑战性更高的部分，即计算新类别ω3的数据与已知类别（ω1和ω2）的投影方向和分类阈值。这涉及到扩展算法以处理更多的类别，展示了Fisher线性判别方法的适应性和灵活性。 整个实验不仅强调了数学上的降维概念，还涉及编程技巧和实际问题解决能力，帮助学习者理解并掌握Fisher线性判别这一统计学在机器学习和数据分析中的核心工具。通过这个过程，参与者不仅能提升数据分析技能，还能深入理解维度减少如何影响模型的性能和复杂度。