平稳时间序列模型构建与识别
需积分: 42 58 浏览量
更新于2024-07-21
收藏 777KB PPT 举报
"平稳时间序列模型的建立"
平稳时间序列模型是统计分析和预测领域中的一个重要概念,尤其在经济、金融、气象学等数据分析中广泛应用。平稳时间序列是指其统计特性(如均值、方差和自相关函数)不随时间变化的序列。这种稳定性使得我们可以基于历史数据有效地预测未来趋势。
在建立平稳时间序列模型的过程中,通常需要经过以下几个步骤:
1. 模型识别:这是建模的第一步,主要是根据时间序列数据的特性来选择合适的模型类型和阶数。对于零均值的平稳序列,ARMA(自回归滑动平均)模型是一种常用的选择。在识别模型时,需要观察序列的趋势、季节性和周期性,并根据这些信息来确定模型的结构。例如,如果序列显示出明显的线性趋势,则可能需要进行差分变换使之变为平稳。
2. 模型定阶:确定模型的阶数,即自回归项(AR)和滑动平均项(MA)的数量。这通常涉及到对自相关函数(ACF)和偏自相关函数(PACF)的分析。ARFIMA(自回归分数差分滑动平均)模型可能适用于具有长期记忆性的非平稳序列。
3. 模型参数估计:一旦模型结构确定,就需要用实际观测数据来估计模型的参数。常用的方法有最大似然估计法或最小二乘法。参数估计的目的是找到最佳的模型系数,使得模型与实际数据尽可能匹配。
4. 模型的诊断检验:这一步是为了验证模型的适用性和合理性。包括检查残差序列的独立性、正态性以及模型的残差自相关图。例如,单位根检验可以用来确认模型是否成功地消除了序列的非平稳性,而拉格朗日乘数检验或Q统计量可用于检测残差的自相关性。
5. 模型的应用:完成以上步骤后,模型可用于预测、滤波或建模后的数据分析。例如,建立好的ARMA模型可以用于生成未来时间点的预测值,帮助决策者制定策略。
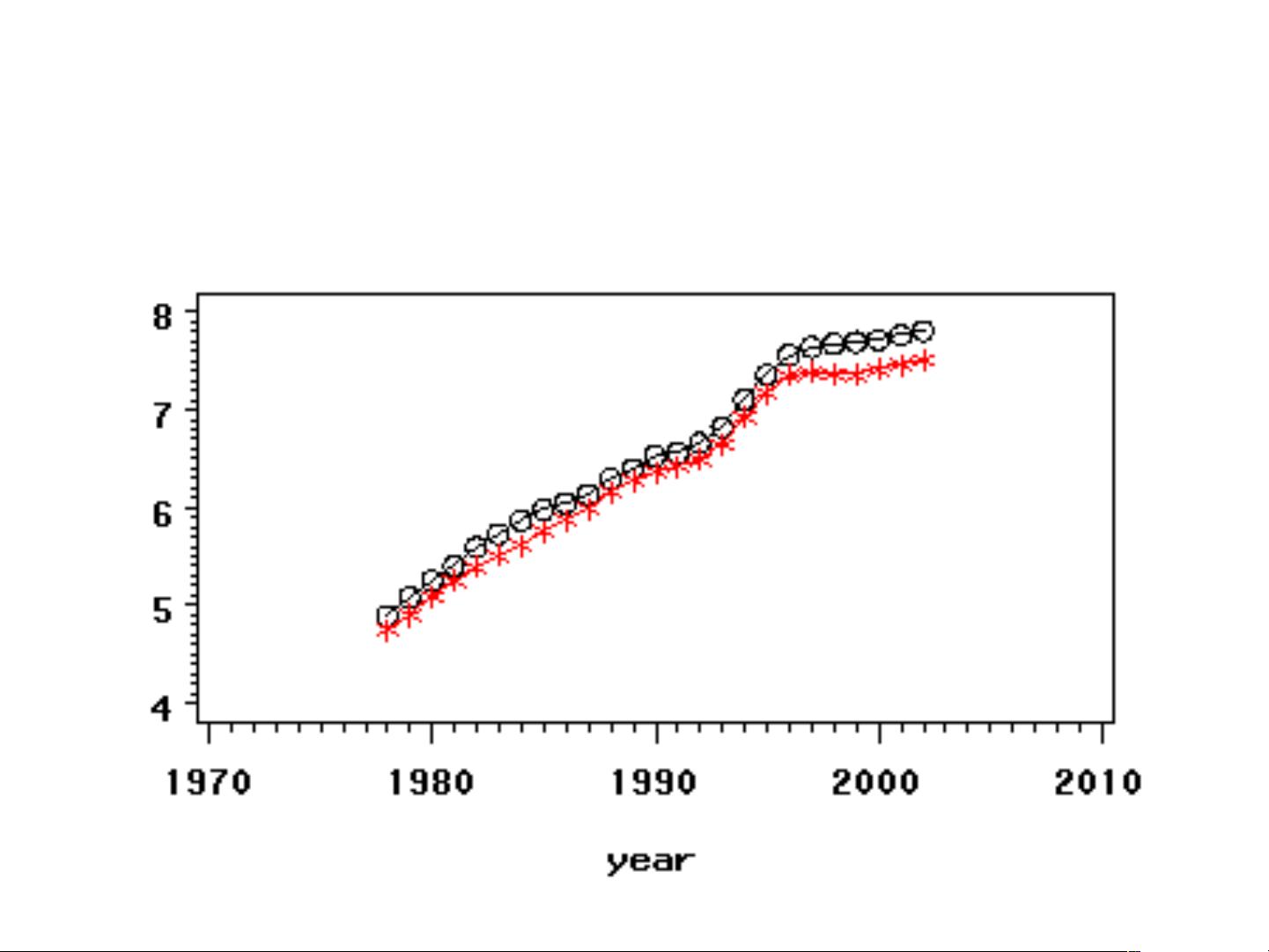
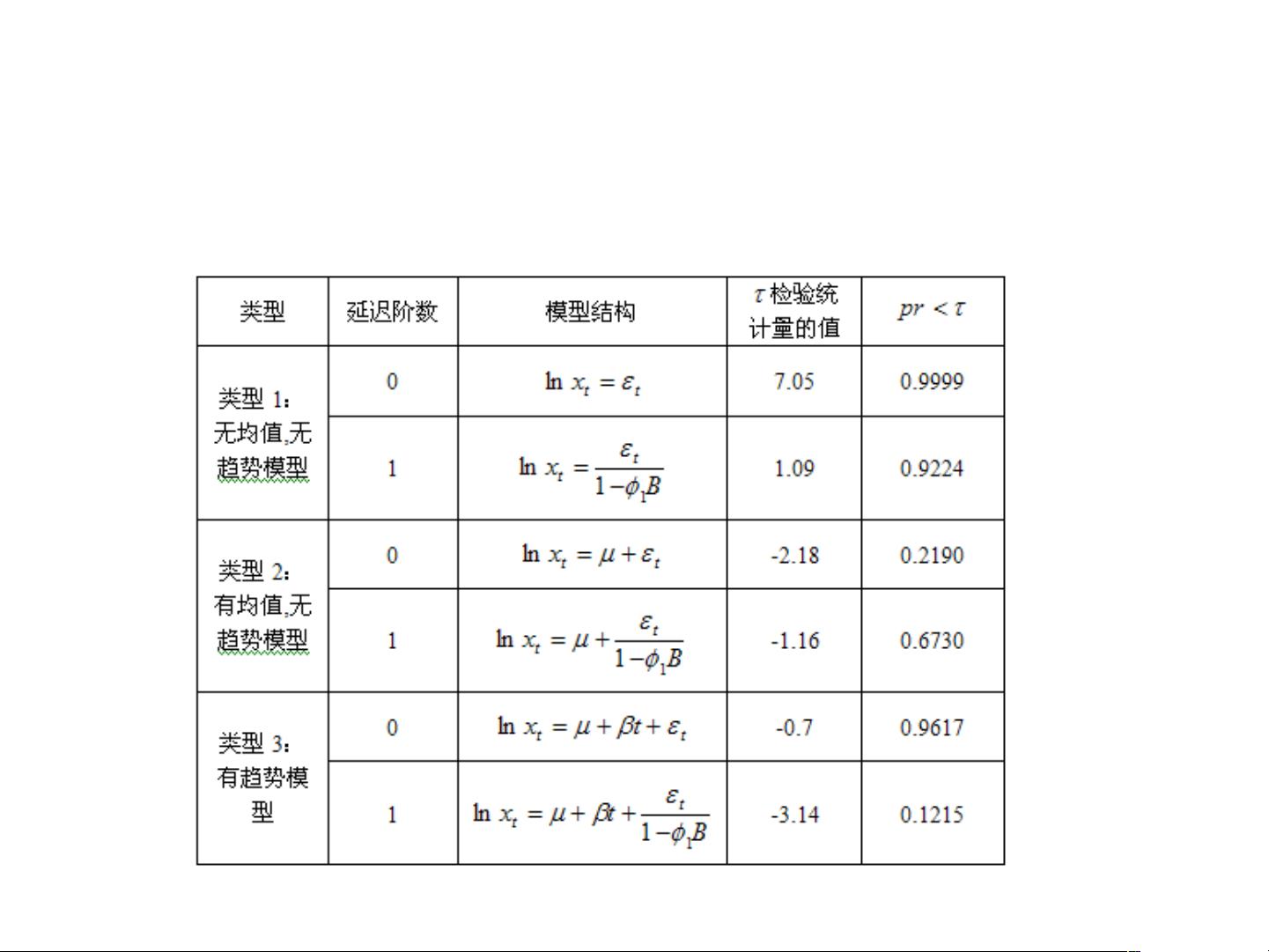
在实际操作中,非平稳序列的处理至关重要。如果序列的均值或方差随时间变化,可以采用差分变换(如一次差分或二次差分)来消除趋势,或者使用对数变换、平方根变换等来稳定方差。单位根检验,如ADF(Augmented Dickey-Fuller)检验、DF(Dickey-Fuller)检验或PP(Phillips-Perron)检验,是判断序列是否平稳的标准工具。这些检验通过计算检验统计量并比较临界值来确定序列是否通过了单位根检验,从而判断其是否平稳。
平稳时间序列模型的建立涉及多个环节,包括模型选择、参数估计和模型诊断,以及对非平稳序列的预处理。理解并熟练掌握这些步骤对于准确地分析和预测时间序列数据至关重要。
2021-10-03 上传
2021-10-23 上传
2021-10-04 上传
2021-10-08 上传
2021-10-07 上传
qq_29281991
- 粉丝: 0
最新资源
- Saber仿真下的简化Buck环路分析与TDsa扫频
- Spring框架下使用FreeMarker发邮件实例解析
- Cocos2d捕鱼达人路线编辑器开发指南
- 深入解析CSS Flex布局与特性的应用
- 小学生加减法题库自动生成软件介绍
- JS颜色选择器示例:跨浏览器兼容性
- ios-fingerprinter:自动化匹配iOS配置文件与.p12证书
- 掌握移动Web前端高效开发技术要点
- 解决VS中OpenGL程序缺失GL/glut.h文件问题
- 快速掌握POI技术,轻松编辑Excel文件
- 实用ASCII码转换工具:轻松实现数制转换与查询
- Oracle ODBC补丁解决数据源配置问题
- C#集成连接器的开发与应用
- 电子书制作教程:你的文档整理助手
- OpenStack计费监控:使用collectd插件收集统计信息
- 深入理解SQL Server 2008 Reporting Services