A*与IDA*搜索算法解析

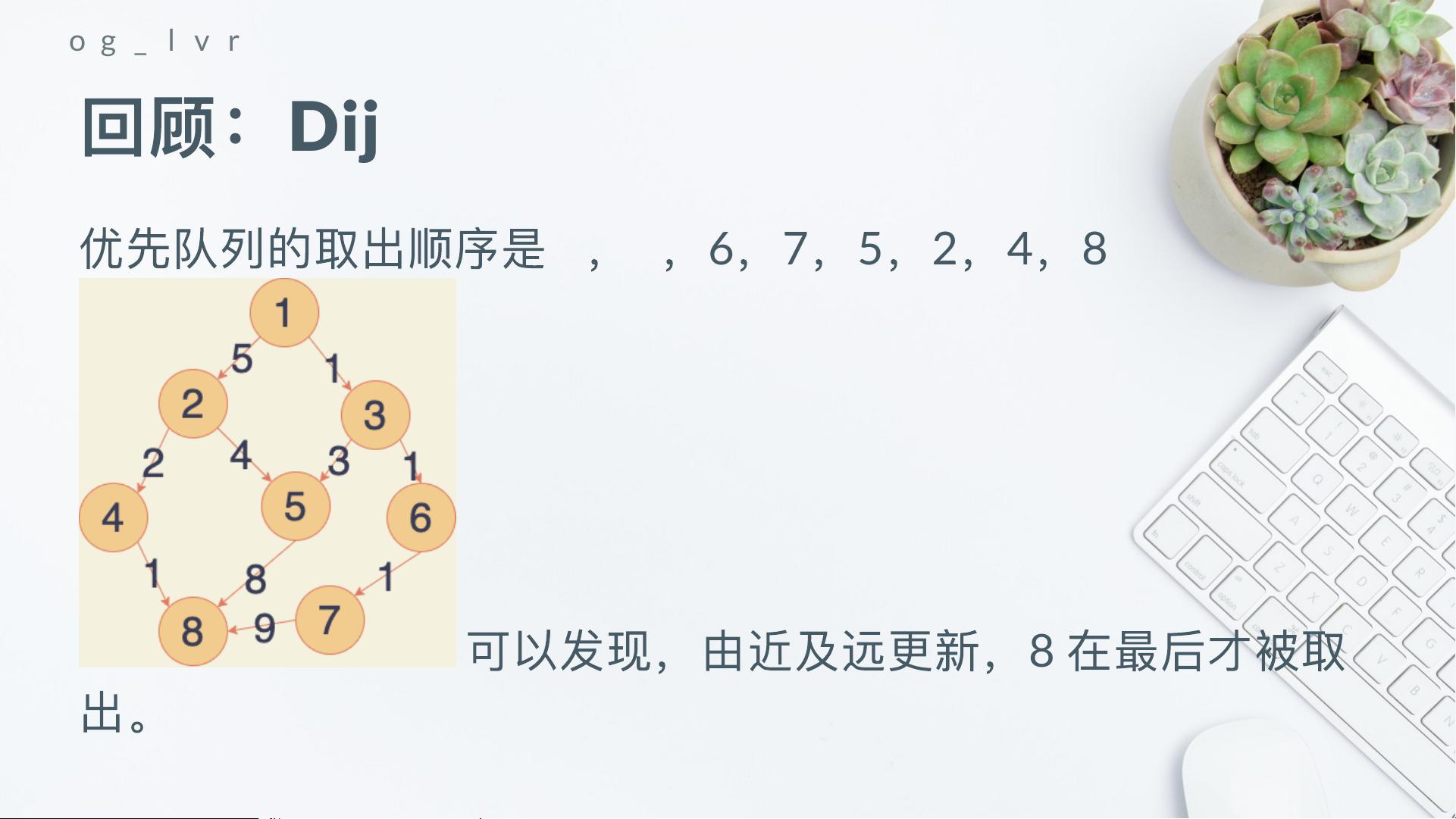
"IDAstar.pdf" 本文主要介绍了两种优化搜索算法：A* 和 IDA*，它们都是在解决路径寻找问题中的重要工具。首先，文章回顾了基础的搜索算法，如宽度优先搜索（BFS）和Dijkstra算法，然后详细讨论了A*启发式搜索以及IDA*的迭代加深深度优先搜索。 1. **宽度优先搜索（BFS）** BFS适用于解决无权图中最短路径问题，因为它保证了最早被发现的节点拥有最短路径。通过使用队列来保持拓扑顺序，BFS可以在找到目标节点时立即得到最优解。 2. **Dijkstra算法** Dijkstra算法适用于非负权重的图，同样用于求解单源最短路径问题。它利用优先队列（通常是二叉堆）按路径长度递增的顺序处理节点，确保每次从队列中取出的节点都已找到其最短路径。算法包括将起点加入队列，然后不断更新并标记节点，直到所有节点都被处理。 3. **A*启发式搜索** A*算法是在Dijkstra算法基础上的优化，它引入了估价函数（f(n) = g(n) + h(n)），其中g(n)是从起点到当前节点的实际路径成本，h(n)是从当前节点到目标的启发式估计成本。通过设计好的估价函数，A*能够更高效地找到最优路径，尤其是在搜索状态空间较大的情况下。 4. **IDA*（迭代加深深度优先搜索）** IDA*是针对深度优先搜索（DFS）的一种优化，尤其适合于解决具有大量可能路径的问题。与普通DFS不同，IDA*通过迭代加深技术限制搜索深度，每次增加深度上限直至找到目标。它也使用估价函数，但目标是在每个深度层找到一条路径，而不是遍历所有可能路径。当达到目标或搜索深度超过预先设定的最大深度时，算法会回溯并尝试更深的搜索。 5. **复杂度和适用场景** BFS和Dijkstra通常适用于边权非负的情况，它们的时间复杂度为O((V+E)logV)，其中V是节点数，E是边数。A*和IDA*则更适合于需要快速找到最优解且空间复杂度较高的情况，它们的效率依赖于估价函数的质量。 6. **最短路问题与搜索问题的对比** 最短路问题通常关注所有点到源点的最短路径，而搜索问题更专注于找到特定目标的最优路径。在某些情况下，搜索算法可以通过调整搜索顺序（如A*和IDA*）来提高效率，同时保证答案的正确性。 总结，A*和IDA*都是在经典搜索算法基础上的优化，它们结合了实际路径成本和启发式估计，以实现更高效的路径搜索。在解决迷宫问题、游戏路径规划等问题时，这两种方法常常能提供优秀的性能。