信息论与编码：限失真信源编码与信息率失真函数

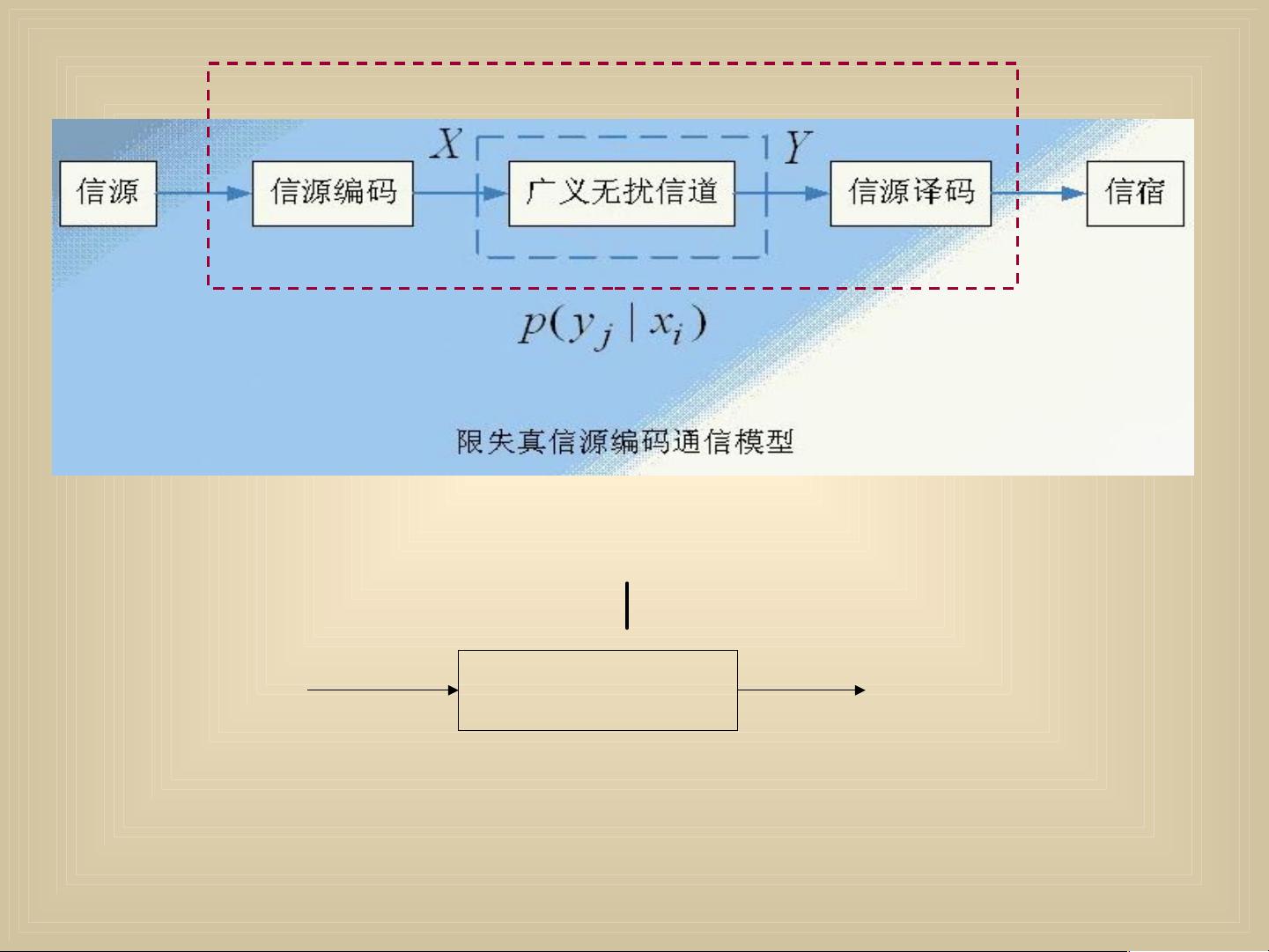
"信息论与编码课程的第五章内容主要涉及限失真信源编码，包括信息率失真函数、限失真信源编码定理以及常见的信源编码方法。" 在信息论中，"信息率失真函数"是研究信源编码时允许一定失真条件下，最小的信息传输速率。这个概念在实际应用中极为重要，因为很多情况下，完全无损的编码并非总是必要的，只要信息的失真控制在可接受范围内即可。这一章首先介绍了"平均失真和信息率失真函数"的概念。 平均失真是衡量信源编码后产生的失真的平均程度。在实际通信系统中，信号的传输往往伴随着失真，但只要失真不超过一定限度，我们仍可以接受。为了量化失真，引入了"失真函数"。失真函数d(xi, yj)用来衡量信源符号xi通过编码变为yj时产生的失真程度。失真函数通常是非负的，并且当xi等于yj时，失真为零，表示无失真。 失真矩阵是由所有可能的信源符号xi和编码符号yj之间的失真函数d(xi, yj)组成的矩阵，它全面展示了所有可能组合的失真情况。例如，在一个简单的例子中，如果信源符号为{0,1}，而编码符号为{0,1,2}，并且定义了特定的失真函数，可以构建相应的失真矩阵。 在5.1节中，还提到了"均方失真"作为一种特定类型的失真度量，它是指信源符号和编码符号之间的平方差的平均值。除此之外，还有其他类型的失真度量，可以根据具体应用场景选择合适的度量方式。 "限失真信源编码定理"是信息论中的一个重要理论，它阐述了在给定的最大允许失真条件下，能够实现的最小信息传输速率。这个定理对于设计有效的编码策略至关重要，因为它指明了在保证一定信息质量的前提下，如何最高效地传输数据。 最后，课程可能会简要介绍一些常见的"信源编码方法"，如霍夫曼编码、算术编码、游程编码等，这些编码技术在实际中被广泛用于压缩数据，同时控制失真在可接受范围内。 信息论与编码的这第五章深入探讨了在允许一定失真的前提下，如何有效地编码信源，以达到最小化信息传输速率的目的，这对于理解和优化通信系统的性能至关重要。