HMM基础与应用：从模型到词性标注

"这份学习资料主要涵盖了HMM（隐马尔科夫模型）的基本概念、应用以及相关的算法，包括词性标注，如马尔科夫链、Baum-Welch算法和Viterbi算法。资料详细阐述了HMM在处理序列数据时的关键任务，如计算观察序列的概率、找到最可能的状态序列以及优化模型参数。" 隐马尔科夫模型（HMM）是一种统计建模方法，常用于自然语言处理和生物信息学等领域。模型的核心思想是，系统处于某种不可见的状态，这些状态只能通过一系列可见的观察值来间接了解。HMM是一个五元组，包含状态集S、初始状态S0、输出字母表Y、转移概率分布PS和发射概率分布PY。 HMM的主要任务包括： 1. 计算观察序列的概率：给定一个HMM模型和一个观察序列，我们希望知道这个序列出现的概率。这在语言模型中尤其重要，可以用来评估一个句子的合理性。 2. 找到最可能的状态序列：Viterbi算法用于解决这个问题，它能找出解释给定观察序列的最有可能的一系列状态。 3. 寻找最佳参数模型：Baum-Welch算法是一种EM（期望最大化）算法，用于在已知观察序列的情况下优化HMM的参数，使其更好地拟合数据。 马尔科夫链是HMM的基础，它假设当前状态只依赖于前一个状态，即状态间的转移概率只与前一个状态有关。例如，Bigram和Trigram模型分别考虑了前两个和前三个状态的影响。在HMM中，每个状态可以产生多种可能的输出，并且这些输出带有概率，使得模型能够处理不确定性。 HMM的一个关键特性是“隐藏性”，即真实状态不直接观测，只能通过观测序列推断。例如，在天气预报中，我们可能只能观察到是否带伞，而无法直接观察天气，但可以通过HMM推测天气情况。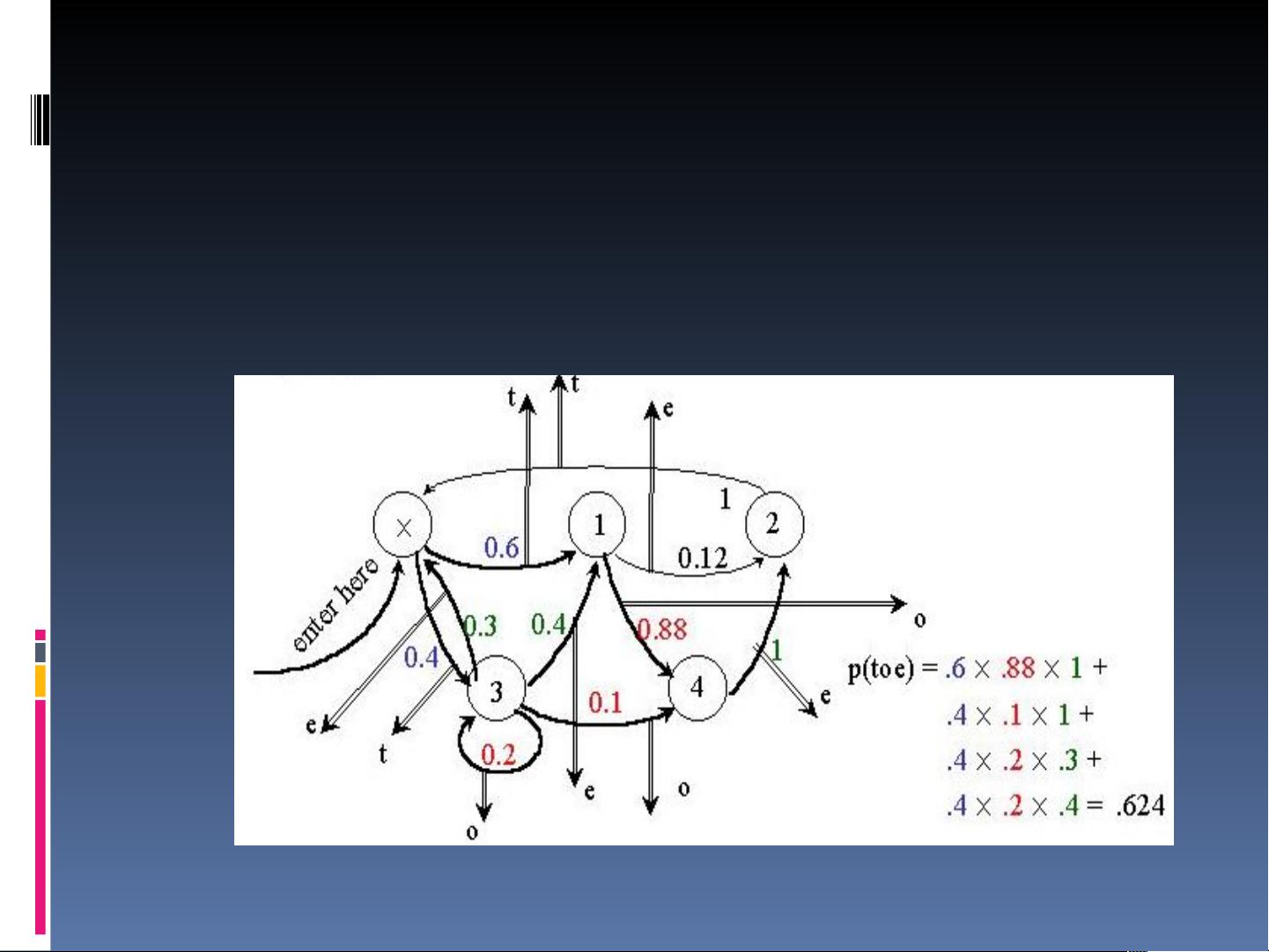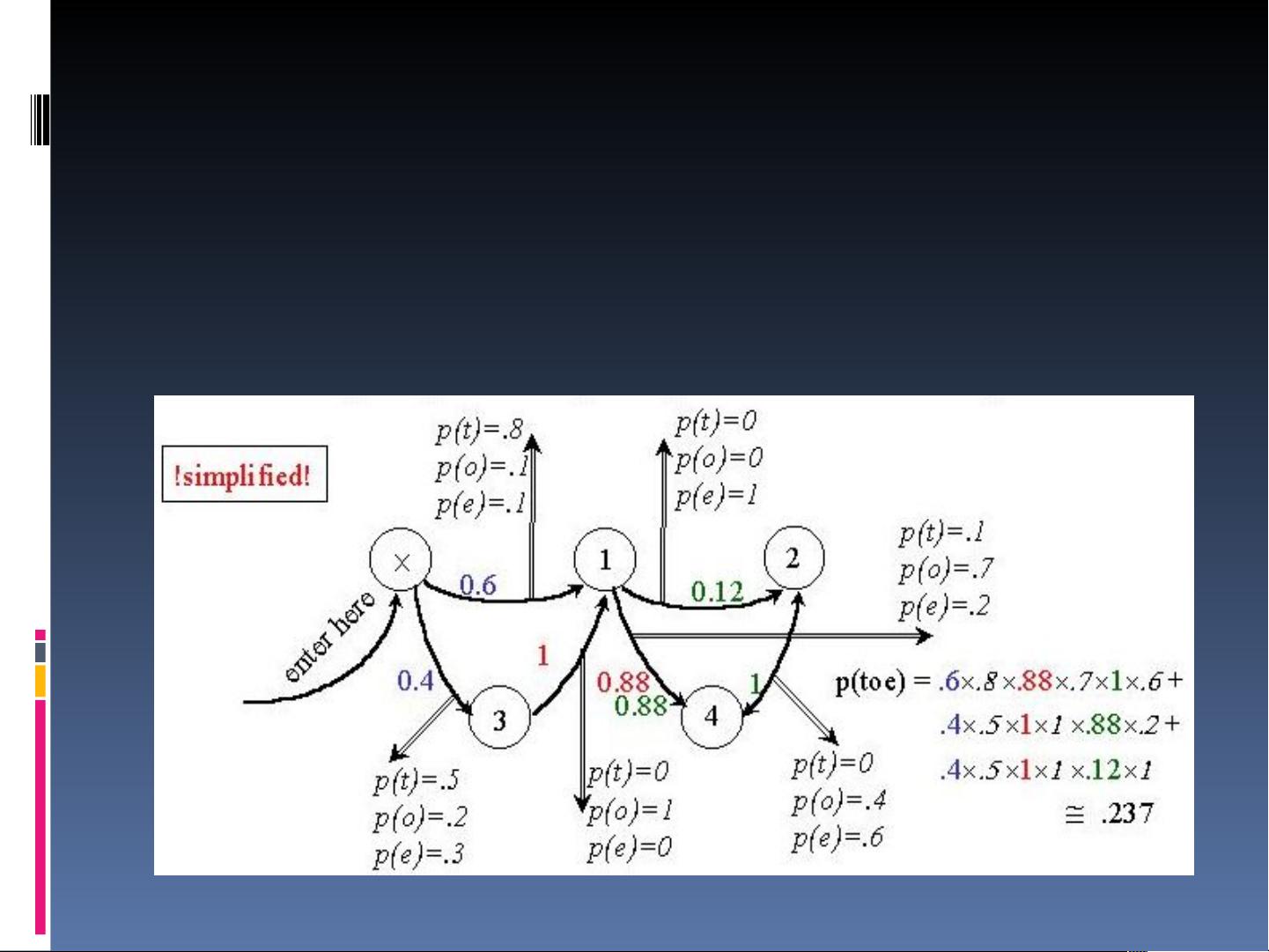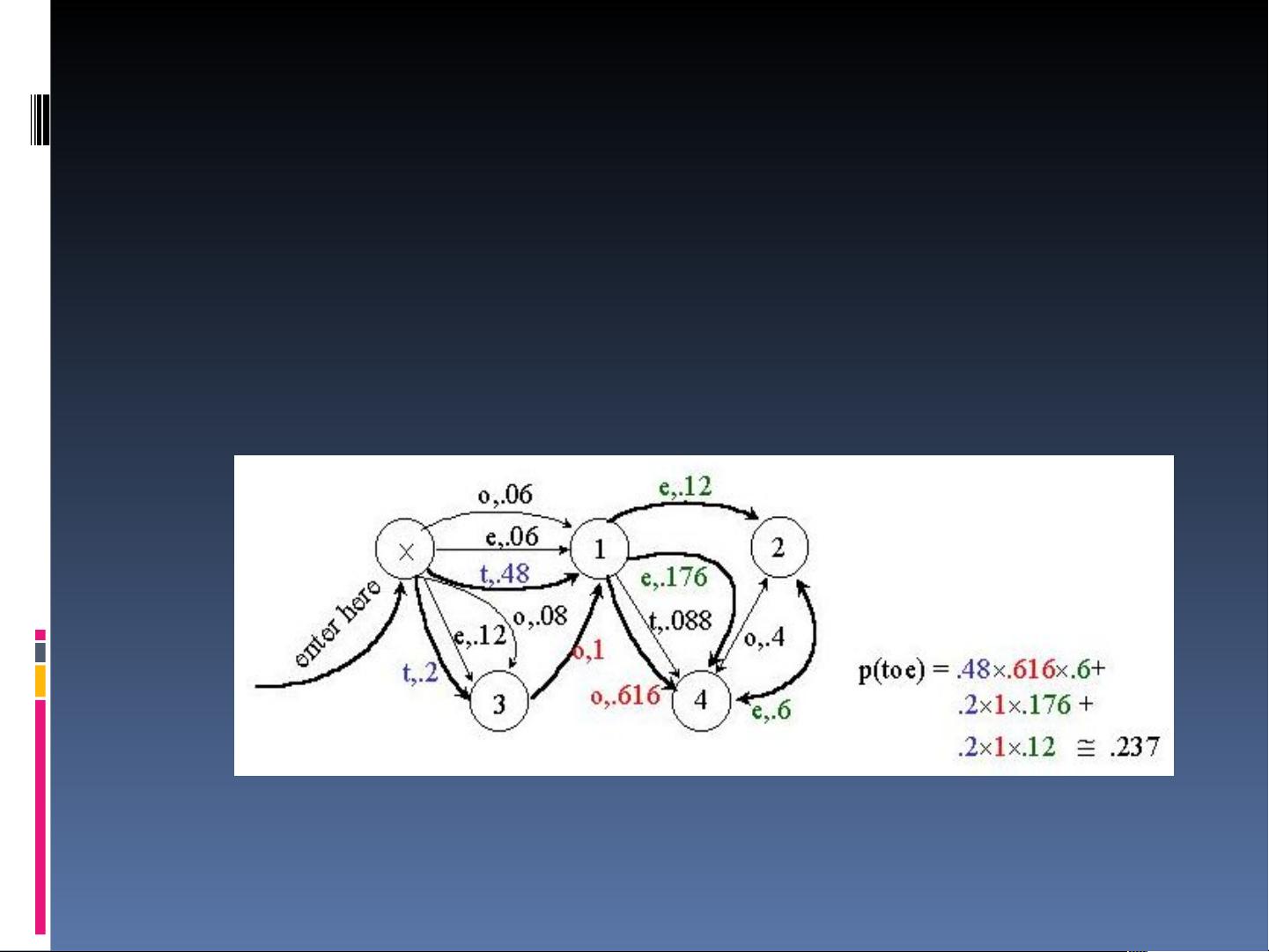 在实际应用中，HMM可以用于词性标注，利用状态（词性）和观察（词）之间的转换概率来分析文本。通过将词分类到更少的类别中，可以缓解数据稀疏问题，提高模型的性能。Trellis图或栅格图是可视化这些概率计算的有效工具，它们显示了不同状态和观察序列的概率路径。 这份学习资料提供了HMM的基础知识，对于初学者来说是一份很好的入门资源，有助于理解HMM的工作原理及其在序列数据分析中的应用。通过学习这些内容，可以为进一步深入研究HMM及相关算法打下坚实的基础。