优化求和效率：树状数组详解与区间划分

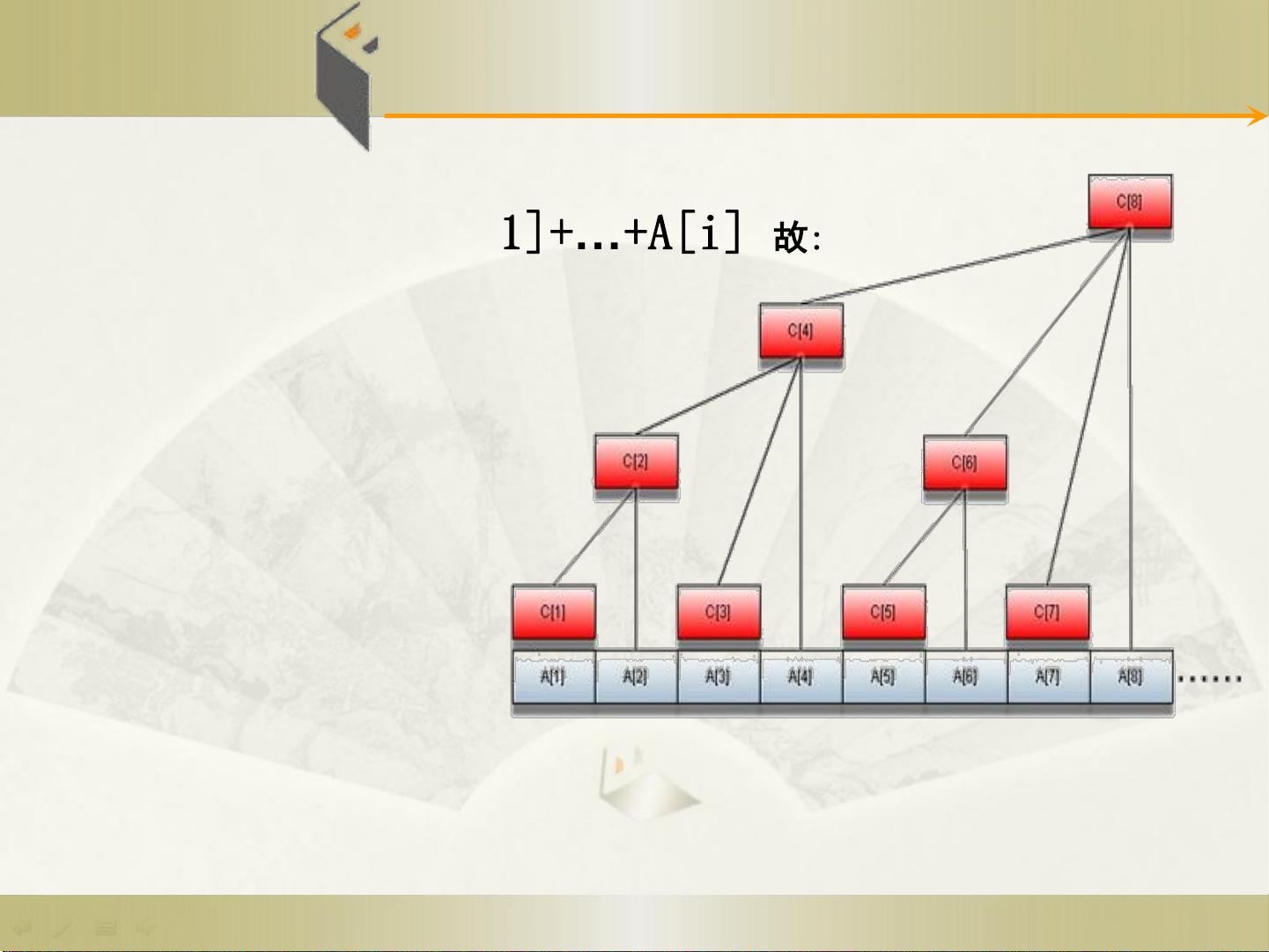
本章节主要讨论的是树状数组（CSP-S）的数据结构和算法，它是一种高效的数据结构，特别适用于处理序列的前缀和问题。在实际应用中，当我们需要频繁地更新和查询一个长度为n的序列A[1]...A[n]的前缀和，例如计算S[i]=A[1]+A[2]+...+A[i]，而这些操作需要在修改任意元素A[i]后快速调整前缀和，传统的暴力方法可能导致O(n)的时间复杂度，对于大规模数据（如n、m>=10000）来说，效率极低。 1. **单点修改**：在树状数组中，修改单个元素A[i]为指定值val的关键在于维护数组C[]的结构，该结构是通过将原序列A[]划分为多个长度为2的幂的区间。每次修改时，只需影响对应的区间，并通过计算得到新的C[i]值，这一步的时间复杂度为O(logn)。 2. **树状数组的构建**：首先，根据任意正整数的二进制表示进行划分，将序列A[]的索引i映射到二进制形式的区间。每个区间长度为2的幂，然后计算每个区间的前缀和并存储在数组C[]中。构建过程利用了C[i] = A[i-2^k+1]+...+A[i]这样的公式，其中k是使得2^k <= i的最小整数，这使得查找和更新操作都只需要对C[]进行O(logn)次操作。 3. **区间和查询**：对于区间[l, r]的和，可以通过计算C[r] - C[l-1]来快速得出，因为C[r]包含了区间[l, r]的所有元素和，减去C[l-1]则消除了前面已知的和。这也同样能在O(logn)时间内完成。 4. **效率提升原因**：暴力求解的瓶颈在于每次计算前缀和时都重新遍历了已计算过的元素。而树状数组通过预先划分区间，实现了局部性，确保了在修改后仅影响相关区间，极大地提高了计算效率。 5. **划分区间的方法**：根据二进制分解原理，任何正整数x都可以唯一表示为2的幂次之和，这使得区间划分成O(logx)个长度为2的幂次部分，每个部分对应数组C[]的一个索引。 总结起来，树状数组是解决大量前缀和计算问题的高效工具，它通过巧妙地组织数据和利用二进制特性，实现了在修改和查询操作中的O(logn)时间复杂度，大大提升了程序的运行速度。这对于处理大数据量的情况尤其重要，是IT领域中优化性能的重要策略之一。